Bài giảng Hình học Lớp 11 - Tiết 33: Đường thẳng vuông góc với mặt phẳng. Bài tập

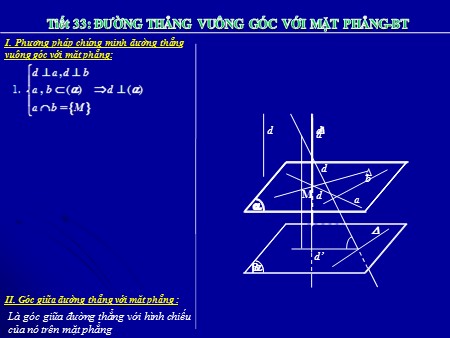
 I. Phương pháp chứng minh đường thẳng 
vuông góc với mặt phẳng:
 da⊥⊥ db,
 1.,()() abd  ⊥ 
 abM= 
 d d 
 d 
 b
 M d a
 d’
  
II. Góc giữa đường thẳng với mặt phẳng :
 Là góc giữa đường thẳng với hình chiếu 
 của nó trên mặt phẳng I. Phương pháp chứng minh đường thẳng a. Chứng minh : SAB, SAC là các tam giác vuông 
vuông góc với mặt phẳng:
 SA ⊥ (ABC) SA ⊥ AB SAB vuông tại A
 da⊥⊥ db, 
 1.,()() abd  ⊥ SA⊥ (ABC) SA⊥ AC SAC vuông tại A
 abM=  b. Chứng minh rằng: BC ⊥ (SAB)
 d // 
 2.() ⊥d ABC vuông tại B BC ⊥ AB BC ⊥ (SAB)
 ⊥() 
 SA ⊥ (ABC) BC ⊥ SA 
 d ⊥ ()
 3.() ⊥d c. Chứng minh rằng AH ⊥ SC
 () / /()
II. Phương pháp chứng minh hai đường ABC vuông tại B BC ⊥ AB
thẳng vuông góc : BC ⊥ (SAB)
 SA ⊥ (ABC) BC ⊥ SA
 d ⊥ () s
 1. ⊥d 
 () 
 dd// /
 2. ⊥d 
 /
 d ⊥ 
 3. Sử dụng tính chất 3 đường vuông 
 góc H
II. Góc giữa đường thẳng với mặt phẳng : a c
 Là góc giữa đường thẳng với hình chiếu 
 của nó trên mặt phẳng B I. Phương pháp chứng minh đường thẳng a. Chứng minh : BC ⊥ (ADI)
vuông góc với mặt phẳng:
 ABC cân tại A có AI là trung tuyến 
 da⊥⊥ db,
 AI là đường cao AI⊥ BC (1)
 1.,()() abd  ⊥ 
 abM=  D B C cân tại D có DI là trung tuyến 
 d // DI là đường cao
 2.() ⊥d 
 ⊥() DIBC⊥ (2)
 d ⊥ ()
 3.() ⊥d Từ (1) (2) BCADI⊥ ()
 () / /()
II. Phương pháp chứng minh hai đường A
thẳng vuông góc :
 d ⊥ () 
 1. ⊥d 
 () 
 dd// /
 2. ⊥d 
 /
 d ⊥ 
 3. Sử dụng tính chất 3 đường vuông 
 B D
 góc
II. Góc giữa đường thẳng với mặt phẳng :
 Là góc giữa đường thẳng với hình chiếu I
 của nó trên mặt phẳng C Cho hình chóp S.ABC có SA ⊥(ABC), ∆ABC 
 BTTN vuông tại B, SA = AB = BC = a. Gọi I là trung 
 điểm của AC.
CÂU 2: Góc (SC, (ABC)) bằng góc 
 nào sau đây?
A. Góc (SC,AC) 
 S
 B. SCB
 a
 C. SBA
 A
 a I
 D. Góc(SC,BC)
 B a C
 Đáp án: A Cho hình chóp S.ABC có SA ⊥(ABC), ∆ABC vuông 
 BTTN tại B, SA = AB = BC = a. I là trung điểm cạnh AC. 
 S Trong mp(ABC) lấy D sao cho ABCD là hình vuông.
 Câu 4: Đường thẳng BD vuông góc 
 với đường nào sau đây?
 A. BC 
 A
 D B. SB 
 I C. SD 
B C D. SC 
 Đáp án: D