Chuyên đề Bồi dưỡng HSG Toán 12 - Bài: Vận dụng nguyên hàm. Tích phân giải quyết 1 số bài Toán thực tế

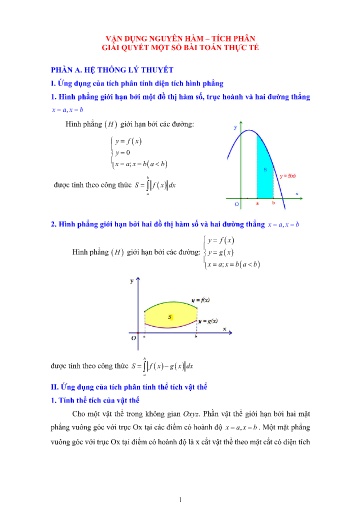
 VẬN DỤNG NGUYÊN HÀM – TÍCH PHÂN 
 GIẢI QUYẾT MỘT SỐ BÀI TOÁN THỰC TẾ 
PHẦN A. HỆ THỐNG LÝ THUYẾT 
I. Ứng dụng của tích phân tính diện tích hình phẳng 
1. Hình phẳng giới hạn bởi một đồ thị hàm số, trục hoành và hai đường thẳng 
 x a, x b 
 Hình phẳng H giới hạn bởi các đường: 
 y f x 
 y 0 
 x a; x b a b 
 b
 được tính theo công thức S f x dx 
 a
2. Hình phẳng giới hạn bởi hai đồ thị hàm số và hai đường thẳng x a, x b 
 y f x 
 Hình phẳng H giới hạn bởi các đường: y g x 
 x a; x b a b 
 b
được tính theo công thức S f x g x dx 
 a
II. Ứng dụng của tích phân tính thể tích vật thể 
1. Tính thể tích của vật thể 
 Cho một vật thể trong không gian Oxyz. Phần vật thể giới hạn bởi hai mặt 
phẳng vuông góc với trục Ox tại các điểm có hoành độ x a, x b . Một mặt phẳng 
vuông góc với trục Ox tại điểm có hoành độ là x cắt vật thể theo mặt cắt có diện tích 
 1 
 là S x . Giả sử S x là hàm số liên tục trên đoạn a; b . Khi đó thể tích V của phần 
 b
vật thể tính bởi công thức V S x dx . 
 a
2. Tính thể tích của khối tròn xoay 
 Cho hàm số y f x liên tục trên đoạn a; b . Gọi H là hình phẳng giới 
hạn bởi các đường 
 y f x 
 y 0 
 x a; x b a b 
 Thể tích khối tròn xoay được sinh ra do hình H xoay quanh trục Ox được 
 b
 2
tính bằng công thức: V f x dx 
 a
III. Ứng dụng của nguyên hàm, tích phân vào thực tế 
 Với một đại lượng f x biến thiên theo biến số x thì tốc độ thay đổi (vận 
tốc) của f x theo biến x chính là đạo hàm f' x (với giả sử rằng f' x luôn tồn tại). 
Ngược lại, khi biết tốc độ thay đổi f' x của một đại lượng f x thì có thể suy ra mô 
hình hàm số biểu thị cho đường đi của đại lượng đó bằng cách lấy nguyên hàm của
 f' x . Nghĩa là: 
 f x f' x dx 
 2 
 Khi biết tốc độ thay đổi f' x của một đại lượng f x . Sự chênh lệch giá 
trị của đại lượng f x trong khoảng giá trị của biến x đi từ a đến b được xác định 
bởi công thức: 
 b
 f b f a f' x dx 
 a
 Đây là mấu chốt quan trọng để giải quyết các bài toán thực tiễn như khi biết 
tốc độ tăng trưởng của một đại lượng, ta có thể tìm một hàm số biểu thị số lượng 
của đại lượng đó qua từng thời kì. Trong thực tế, nhiều bài toán liên quan tới nội 
dung này có thể kể đến như: sự chuyển động của vật, sự gia tăng dân số, sự phát 
triển của vi khuẩn, các bài toán về sản xuất và kinh doanh 
1. Bài toán về chuyển động 
 + Giả sử vật M chuyển động trên quãng đường có độ dài là s trong khoảng thời 
 v
gian t. Khi đó, vật M chuyển động với vận tốc trung bình là s 
 t
 + Tuy nhiên, chúng ta gặp rất nhiều trường hợp vật chuyển động không đều, 
vận tốc thay đổi liên tục tùy theo vị trí và thời gian. Ví dụ xe chạy trên đường gặp 
nhiều chướng ngại vật thì giảm tốc, chạy trên đường thông thoáng thì tăng tốc. Vì 
vậy ta cần phương pháp tính đúng vận tốc của xe tại mỗi thời điểm. 
 + Giả sử v(t) là vận tốc của vật M tại thời điểm t, và s(t) là quãng đường vật đi 
được sau khoảng thời gian t tính từ lúc bắt đầu chuyển động. Ta có mối liên hệ giữa 
s(t) và v(t) 
 Đạo hàm của quãng đường là vận tốc: 
 s' t v t 
 Nguyên hàm của vận tốc là quãng đường: 
 s t v t dt 
 + Từ đây ta cũng có quãng đường vật đi được trong khoảng thời gian
 t  a; blà: 
 b
 s v t dt 
 a
 + Nếu gọi a(t) là gia tốc của vật M thì ta có mối liên hệ giữa v(t) và a(t) 
 Đạo hàm của vận tốc chính là gia tốc 
 v' t a t 
 Nguyên hàm của gia tốc chính là vận tốc 
 3 
 v t a t dt 
2. Bài toán về tăng trưởng, phát triển 
 Cho hàm số f x biểu diễn cho sự tăng (hay giảm) số lượng của một đối tượng 
nào đó ( số người, vi khuẩn, vi trùng, lượng nước chảy, ) 
 Giá trị f x là số lượng của đối tượng đó tại thời điểm x. 
 Đạo hàm f' x chính là tốc độ tăng (hay giảm) của đối tượng đó tại thời điểm 
x. 
 Số lượng tăng thêm( hoặc giảm đi) của đối tượng trong khoảng x  a; b là: 
 b
 f' x dx 
 a
PHẦN B. MỘT SỐ BÀI TẬP ÁP DỤNG 
Bài 1. Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân 
cổng là AB 8 m . Người ta treo một tâm phông hình chữ nhật có hai đỉnh MN, nằm 
trên Parabol và hai đỉnh PQ, nằm trên mặt đất (như hình vẽ), biết 
 MN 4 m , MQ 6 m .Ở phần phía ngoài phông (phần không tô đậm) người ta mua 
hoa để trang trí hoa, biết chi phí để trang trí hoa là 200000 đồng/ m2 . Tính số 
tiền(triệu đồng) để trang trí hoa (phần không tô đậm)(kết quả làm tròn đến hàng 
phần trăm). 
Phân tích bài toán: 
 + Chọn hệ trục toạ độ Oxy sao cho hai điểm A, B nằm trên trục Ox ( như 
hình vẽ bên dưới). 
 + Parabol đối xứng qua Oy nên có dạng P :. y ax2 c Vì P đi qua 
 B 4;0 và N 2;6 nên chúng ta tìm được phương trình của parabol (P). 
 + Diện tích của chiếc cổng là phần hình phẳng giới hạn bởi đồ thị hàm số 
 P : y ax2 c , trục hoành và hai đường thẳng x 4; x 4 . Diện tích của cổng tính 
 4
được theo công thức: S ax2 c dx . 
 1 
 4
 4 
 4
 + Diện tích của phần trang trí hoa là: S S S ax2 c dx 24 . 
 1 MNPQ 
 4
 Từ đó ta tính được số tiền để trang trí hoa. 
Hướng dẫn giải: 
 Diện tích của phần phía ngoài phông (phần không tô đậm) bằng diện tích 
hình giới hạn bởi parabol trừ đi diện tích phông hình chữ nhật MNPQ 
 2
Diện tích của hình chữ nhật là: S1 4.6 24 m . 
 Chọn hệ trục tọa độ Oxy như hình vẽ. 
 Parabol đối xứng qua Oy nên có dạng P :. y ax2 c Vì P đi qua B 4;0 
 1
và N 2;6 nên P : y x2 8. 
 2
 Diện tích hình phẳng giới hạn bởi P và trục Ox là:
 4
 12 128 2
 S 2 x 8 d x m . 
 0 2 3
 128 56
Diện tích phần phía ngoài phông để trang trí hoa là S S S 24 m2 . 
 1 MNPQ 3 3
 56
 Vậy số tiền để trang trí hoa(phần không tô đậm) là .0, 2 3,73 (triệu 
 3
đồng) 
Bài 2. Một mảnh đất hình chữ nhật có chiều dài 60m , chiều rộng 20 m . Người ta 
muốn trồng cỏ ở hai đầu của mảnh đất hai hình bằng nhau giới hạn bởi hai đường 
parabol có hai đỉnh cách nhau 40 m (như hình vẽ bên dưới). Phần còn lại của mảnh 
đất người ta lát gạch. Biết chi phí lát gạch là 220000 đồng/ m2 và tiền nhân công 
trồng cỏ là 80000 đồng/ m2 . Tính tổng số tiền để lát gạch và trồng cỏ trên mảnh đất 
đó (làm tròn kết quả đến hàng đơn vị, đơn vị triệu đồng). 
 5 
Phân tích bài toán: 
 + Chọn hệ trục toạ độ như hình vẽ bên dưới. 
 + Diện tích phần mảnh đất để lát gạch bằng diện tích mảnh đất hình chữ 
nhật trừ đi diện tích phần mảnh đất trồng cỏ. 
 + Để tính diện tích phần mảnh đất trồng cỏ ta đi viết phương trình đường 
parabol (P): y ax2 bx c đi qua ba điểm O, F, C và sử dụng tích phân để tính. 
 Diện tích phần mảnh đất tròng cỏ được tính theo công thức: 
 20
 S 2 ax2 bx c dx 
 1 
 0
 + Diện tích phần mảnh đất để lát gạch là SSS2 ABCO 1 
 Từ đó tính được tổng số tiền để lát gạch và trồng cỏ trên mảnh đất 
Hướng dẫn giải: 
Chọ hệ trục tọa độ như hình vẽ 
 Tọa độ các điểm: OABCEF 0;0 , 0;60 , 20;60 , 20;0 ; 10;50 ; 10;10 
 Parabol P có đỉnh F 10;10 , có phương trình dạng: y ax2 bx c 
 1
 a 
 400a 20 b 0 10
 P đi qua O 0;0 và C 20;0 100a 10 b 10 b 2 
 c 0 c 0
 6 
 1
 Vậy P : y x2 2 x 
 10
 20
 12 800 2
 Diện tích trồng cỏ là S1 2 x 2 x dx m 
 0 10 3
 800 2800 2
 Diện tích lát gạch: S2 20.60 S 1200 m 
 3 3
 2800 800
 Tổng số tiền để lát gạch và trồng cỏ là: .0, 22 .0,08 227 (triệu 
 3 3
 đồng). 
Bài 3. Một ô tô đang chạy với tốc độ 108km / h thì người lái xe bất ngờ phát hiện 
chướng ngại vật trên đường. Người lái xe phản ứng một giây sau đó bằng cách đạp 
phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ 
 v t 10 t 40 m / s , trong đó t là thời gian tính bằng giây kể từ lúc đạp phanh. 
Gọi s t là quãng đường xe ô tô đi được trong t s kể từ lúc đạp phanh. 
a) Công thức biểu diễn hàm số s t 5 t2 40 t m . 
b) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 6 giây. 
c) Sau 4 giây kể từ lúc đạp phanh, quãng đường xe ô tô di chuyển được là 80 m . 
d) Quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại 
vật trên đường đến khi xe ô tô dừng hẳn là 110 m . 
Phân tích bài toán: 
 A B C
 + Đổi 108km / h 30 m / s 
 + Gọi A là vị trí người lái xe phát hiện chướng ngại vật, B là vị trí người 
lái xe đạp phanh, C là vị trí ô tô dừng hẳn. 
 + Từ lúc người lái xe phát hiện chướng ngại vật đến lúc người lái xe đạp 
phanh ô tô đi được quãng đường AB 30.1 30 m . 
 + Quãng đường ô tô đi được trong t giây kể từ lúc người lái xe đạp phanh 
là s t v t dt . 
 + Ô tô dừng hẳn khi v t 0 t 4 
 + Quãng đường ô tô đi được trong 4 giây kể từ lúc đạp phanh là: 
 4
 BC v t dt 
 0
 7 
 + Quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện 
chướng ngại vật trên đường đến khi xe ô tô dừng hẳn bằng quãng đường AB cộng 
với quãng đường BC. 
Hướng dẫn giải: 
a) Ta có : s t v t d t 10 t 40 d t 5 t2 40 t C . 
 Do s 0 0 nên C 0 . 
 Vậy s t 5 t2 40 t m . 
 Chọn đúng 
b) Xe ô tô dừng hẳn khi v t 0 10 t 40 0 t 4 . 
 Chọn sai 
c) Sau 4 giây kể từ lúc đạp phanh, quãng đường xe ô tô di chuyển được là 
 4 4
 BC v t dt 10 t 40 dt 80 m 
 0 0
 Chọn đúng 
d) Ta có 108km / h 30 m / s . 
 Vậy quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện 
chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là 30 80 110 m . 
 Chọn đúng 
Bài 4. Chủ một trung tâm thương mại muốn cho thuê một số gian hàng với giá như 
nhau. Người đó muốn tăng giá cho thuê của mỗi gian hàng thêm x (triệu đồng) 
 x 0 . Tốc độ thay đổi doanh thu từ các gian hàng đó được biểu diễn bởi hàm số 
 T x 20 x 300, trong đó T x tính bằng triệu đồng (Nguồn: R.Larson anh B. 
Edwards, Calculus 10e, Cengage). Biết rằng nếu người đó tăng giá thuê cho mỗi 
gian hàng thêm 10 triệu đồng thì doanh thu là 12 000 triệu đồng. 
a) Doanh thu của tất cả gian hàng được biểu diễn bởi hàm số 
 T x 10 x2 300 x 10000. 
b) Doanh thu của tất cả gian hàng khi người đó tăng giá thêm 12 triệu đồng là 12250 
triệu đồng. 
c) Doanh thu cao nhất của tất cả gian hàng mà người đó có thể thu về là 12250 triệu 
đồng. 
d) Để doanh thu cao nhất của tất cả gian hàng thì mỗi gian hàng đã tăng giá cho thuê 
thêm 15 triệu đồng. 
Phân tích bài toán: 
 8 
 + Doanh thu khi tăng giá cho thuê của mỗi gian hàng thêm x (triệu đồng) 
là nguyên hàm của hàm tốc độ thay đổi doanh thu. Nếu gọi T x là doanh thu khi 
tăng giá cho thuê của mỗi gian hàng thêm x (triệu đồng) thì 
 T x T' x dx 20 x 300 dx 10 x2 300 x C . 
 + Người đó tăng giá thuê cho mỗi gian hàng thêm 10 triệu đồng thì doanh 
thu là 12 000 triệu đồng nên T 10 12000 từ đó tìm được C. 
Hướng dẫn giải: 
a) Gọi T x là doanh thu khi tăng giá cho thuê của mỗi gian hàng thêm x (triệu 
đồng). Ta có T x T' x dx 20 x 300 dx 10 x2 300 x C . 
 Vì TCC 10 12000 10.102 300.10 12000 10000 . 
 Vậy T x 10 x2 300 x 10000. 
 Chọn đúng. 
b) Doanh thu của tất cả gian hàng khi người đó tăng giá thêm 12 triệu đồng là: 
 T 12 12160 (triệu đồng). 
 Chọn sai 
c) Ta có: T x 10 x2 300 x 10000 10 x 152 1225 12250 
Doanh thu cao nhất của tất cả gian hàng mà người đó có thể thu về là 12250 triệu 
đồng khi mỗi gian hàng đã tăng giá cho thuê thêm 15 triệu đồng. 
 Chọn đúng 
d) Chọn đúng 
Bài 5. Một nghiên cứu chỉ ra rằng sau x tháng kể từ bây giời, dân số của thành phố 
A sẽ tăng với tốc độ v x 10 2 2 x 1 (người/tháng). Hỏi dân số của thành phố sẽ 
tăng bao nhiêu trong 5 tháng tới? (Nguồn: CPO – Tạp chí và tư liệu toán học) 
Phân tích bài toán: 
 + Nguyên hàm của v x chính là hàm số f x biểu thị cho dân số của 
thành phố A sau x tháng kể từ bây giờ. 
 + Đề bài yêu cầu tính dân số tăng thêm của thành phố trong vòng 5 tháng 
tới. Theo lý thuyết đã nêu thì dân số tăng thêm được tính theo công thức: 
 9 
 5
 v x dx f 5 f 0 
 0
Hướng dẫn giải: 
 Gọi f x là dân số của thành phố sau x tháng kể từ bây giờ. 
 Tốc độ thay đổi của dân số là v x 10 2 2 x 1 
 Số dân tăng thêm trong 5 tháng tới của thành phố là: 
 5 5
 f 4 f 0 v x dx 10 2 2 x 1 dx 74 (người) 
 0 0
Bài 6. Trong một đợt xả lũ, nhà máy thuỷ điện A đã xả lũ trong 40 phút với tốc độ 
lưu lượng nước tại thời điểm t giây là v t 10 t 500 m3 / s . Hỏi sau thời gian xả 
lũ trên thì hồ chứa nước của nhà máy đã thoát đi một lượng nước là bao nhiêu? 
(Nguồn: CPO – Tạp chí và tư liệu toán học) 
Phân tích bài toán: 
 + Trong 40 phút, nhà máy thuỷ điện xả lũ với tốc độ v t 10 t 500 m3 / s 
 + Hàm số f t biểu thị cho lượng nước đã xả tại thời điểm t chính là 
nguyên hàm của hàm v t . 
 + Lượng nước xả được trong thời gian 40 phút ( ứng với 2400 giây) là: 
 2400
 f 2400 f 0 v t dt 
 0
Hướng dẫn giải: 
 Lượng nước lũ đã xả trong khoảng thời gian 40 phút (2400 giây) là: 
 2400 2400
 L v t dt 10 t 500 dt 30.106 ( m 3 ) 
 1 1
 Vậy trong khoảng thời gian 40 phút, nhà máy đã xả một lượng nước là 30 
triệu khối nước. 
 10 
 PHẦN C. BÀI TẬP TỰ LUYỆN 
Bài 1. Một quần thể vi khuẩn A có số lượng cá thề là P t sau t phút quan sát được 
phát hiện thay đổi với tốc độ là: P t ae0.1t 150 e 0.03 t (vi khuẩn/phút) a  . Biết 
rằng lúc bắt đầu quan sát, quần thể có 200000 vi khuẩn và đạt tốc độ tăng trường là 
350 vi khuẩn/phút. 
a) Giá trị của a 200 . 
b) P t 2000 e0.1t 5000 e 0.03 t 200000 . 
c) Sau 12 phút số lượng vi khuẩn trong quần thề là 206152 con (làm tròn kết quả 
đến hàng đơn vị). 
d) Sau 12 phút, một quần thể vi khuẩn B có tốc độ tăng trưởng là G t 500 e0.2t (vi 
khuẩn/phút) bắt đầu cạnh tranh nguồn thức ăn trực tiếp với quần thể A. Một cá thể 
tại quần thể B triệt tiêu một cá thể tại quần thể A. Sau 5 phút cạnh tranh quần thể A 
bị triệt tiêu hoàn toàn. Số lượng vi khuần của quần thể B ở thời điềm bắt đầu cạnh 
tranh là 191967 con. (làm tròn kết quả đến hàng đơn vị) 
Bài 2. Một ô tô bắt đầu chuyển động thẳng nhanh dần đều với tốc độ v t 5 t ( m / s ); 
trong đó t là thời gian tính bằng giây kể từ khi ô tô bắt đầu chuyển động. Đi được 6 
(s) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động 
chậm dần đều với gia tốc a 5 ( m / s2 ) . 
a) Tốc độ của ô tô tại thời điểm 10 (s) tính từ lúc xuất phát là 10 (m / s ). 
b) Quãng đường ô tô chuyển động được trong 6 giây đầu tiên là 80 m . 
c) Quãng đường S mà ô tô chuyển động được kể từ lúc bắt đầu đạp phanh đến khi 
 6
dừng lại được tính theo công thức S 30 5t dt . 
 0
d) Quãng đường ô tô chuyển động được kể từ lúc bắt đầu chuyển động cho đến khi 
dừng lại là 170m . 
Bài 3. Một ô tô chuyển động nhanh dần đều với vận tốc được tính theo thời gian t 
bằng v t 8 t ( m / s ). 
a) Gia tốc chuyển động của ô tô là 8 m / s2 . 
b) Vận tốc tại thời điểm 10 giây là v 80 m / s . 
c) Quãng đường ô tô đi được trong khoảng thời gian 4 giây đầu tiên là 96 m. 
 11 
 d) Giả sử ô tô đó đi được 10 giây thì gặp chướng ngại vật và phanh gấp, ô tô tiếp tục 
chuyển động chậm dần đều với gia tốc a 40( m / s2 ). Khi đó quãng đường ô tô đi 
được từ lúc bắt đầu chuyển động đến lúc dừng hẳn là 480 m. 
Bài 4. Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao 
tốc. Khi ô tô cách điểm nhập làn 240 m, tốc độ của ô tô là 28,8 km/h . Bốn giây sau 
đó, ô tô bắt đầu tăng tốc với tốc độ v( t ) at b (m/s) với (a , b , a 0) , trong đó  
là thời gian tính bằng giây kể từ khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc 
sau 16 giây và duy trì sự tăng tốc trong 30 giây kể từ khi bắt đầu tăng tốc. 
a) Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 208 m. 
b) Giá trị của  là 8. 
c) Quãng đường S() t (đơn vị: mét) mà ô tô đi được trong thời gian  giây 
 30
 (0 t 30) kể từ khi tăng tốc được tính theo công thức S()() t v t dt . 
 0
d) Sau 30 giây kể từ khi tăng tốc, tốc độ của ô tô không vượt quá tốc độ tối đa cho 
phép là 100km / h . 
Bài 5. Bác Bình muốn làm một cái cổng hình Parabol như hình vẽ bên dưới. Chiều 
cao GH 4 m , chiều rộng AB 4 m , AC BD 0,9 m . Bác Bình muốn làm hai cánh 
cổng khi đóng lại là hình chữ nhật CDEF tô đậm có giá là 1200000 đồng /m2 , còn 
 2
các phần để trắng làm xiên hoa có giá là 900000 đồng /m . Hỏi tổng số tiền để làm 
hai phần nói trên là bao nhiêu? (Kết quả quy tròn đến hàng đơn vị, đơn vị tính là 
triệu đồng) 
Bài 6. Người ta dự định lắp kính cho cửa của một mái vòm có dạng hình parabol. 
Biết rằng vòm cửa cao 21m , rộng 70m và chi phí để hoàn thiện một mét vuông 
kính là 900 000 đồng (Hình bên dưới). Tính chi phí để lắp kính cho cửa của mái 
vòm đó. (Đơn vị tính theo triệu đồng) 
 12 
Bài 7. Một biển quảng cáo có dạng hình elip với bốn đỉnh AABB1,,, 2 1 2 như hình vẽ 
bên dưới. Biết chi phí để sơn phần tô đậm là 200 000 đồng và phần còn lại là 100000
đồng. Biết A1 A 2 8 m , B 1 B 2 6 m và tứ giác MNPQ là hình chữ nhật có MQ 3 m . Hỏi 
số tiền để sơn theo cách trên (làm tròn đến hàng phần chục, đơn vị triệu đồng) bằng 
bao nhiêu? 
 Qua việc tìm hiểu và giải quyết một số bài toán thực tế bằng phương pháp 
nguyên hàm và tích phân, ta có thể thấy rõ được tính ứng dụng cao và vai trò quan 
trọng của các kiến thức toán học trong đời sống và các ngành khoa học khác. Không 
chỉ dừng lại ở việc rèn luyện kỹ năng tính toán, việc vận dụng nguyên hàm – tích 
phân còn giúp học sinh phát triển tư duy mô hình hóa, khả năng phân tích và giải 
quyết vấn đề một cách linh hoạt, sáng tạo. 
 Hy vọng rằng, thông qua việc tiếp cận các tình huống thực tế, học sinh sẽ 
cảm nhận được tính gần gũi và thiết thực của toán học, từ đó nâng cao sự yêu thích 
và động lực học tập môn học này. Đồng thời, đây cũng là cơ hội để giáo viên đổi 
mới phương pháp giảng dạy, hướng tới việc phát triển năng lực toàn diện cho học 
sinh, đáp ứng yêu cầu của giáo dục hiện đại. 
 13