Đề kiểm tra giữa học kì I Toán 12 - Năm học 2022-2023 - Trường THPT Trần Nguyên Hãn (Có đáp án)

 SỞ GIÁO DỤC VÀ ĐÀO TẠO HẢI PHÒNG KIỂM TRA CHUNG GIỮA HỌC KÌ I 
 TRƯỜNG THPT TRẦN NGUYÊN HÃN LỚP 12 - NĂM HỌC 2022-2023 
 Môn: TOÁN 
I.PHẦN THI TRẮC NGHIỆM ( 7 điểm ). 
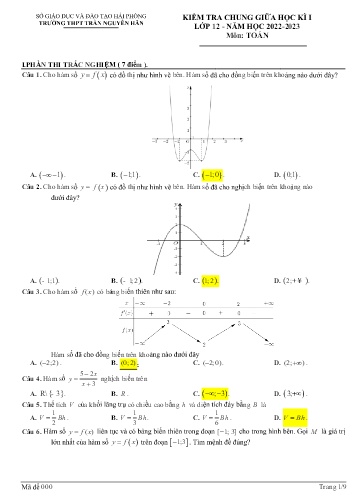
Câu 1. Cho hàm số y f x có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? 
 A. 1 . B. 1;1 . C. 1;0 . D. 0;1 . 
Câu 2. Cho hàm số y= f( x) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào 
 dưới đây? 
 A. (- 1;1) . B. (- 1;2) . C. (1;2) . D. (2;+¥ ) . 
Câu 3. Cho hàm số fx() có bảng biến thiên như sau: 
 Hàm số đã cho đồng biến trên khoảng nào dưới đây 
 A. ( 2;2) . B. (0;2) . C. ( 2;0) . D. (2; ) . 
 52 x
Câu 4. Hàm số y nghịch biến trên 
 x 3
 A. R\{- 3}. B. R . C. ;3 . D. 3; . 
Câu 5. Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 
 1 1 1
 A. V Bh . B. V Bh . C. V Bh . D. V Bh . 
 2 3 6
Câu 6. Hàm số y f() x liên tục và có bảng biến thiên trong đoạn [ 1; 3] cho trong hình bên. Gọi M là giá trị 
 lớn nhất của hàm số y f x trên đoạn  1;3 . Tìm mệnh đề đúng? 
Mã đề 000 Trang 1/9 
 A. Mf ( 1). B. Mf 3 . C. Mf (2) . D. Mf (0) . 
Câu 7. Cho hàm số fx có bảng biến thiên như sau 
Điểm cực đại của hàm số đã cho là 
 A. x 2. B. x 3. C. x 1. D. x 3. 
Câu 8. Cho hàm số y f x liên tục trên R, bảng xét dấu của fx như sau 
 Số điểm cực trị của hàm số đã cho là 
 A. 0 . B. 2 . C. 1. D. 3 . 
Câu 9. Cho hàm số fx có bảng biến thiên như sau 
 Điểm cực đại của hàm số đã cho là 
 A. x 3. B. x 1. C. x 2 . D. x 2. 
Câu 10. Cho hàm số fx() có bảng biến thiên như sau: 
 Hàm số đạt cực tiểu tại: 
 A. x 2. B. x 3. C. x 1. D. x 2 . 
 14 x
Câu 11. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y . 
 21x 
 1
 A. y 2. B. y 4. C. y . D. y 2 . 
 2
Câu 12. Cho hàm số y= f() x có limfx ( )= 3 và limfx ( )=- 3 . Khẳng định nào sau đây là khẳng định đúng 
 x® + ¥ x® - ¥
 ? 
 A. Đồ thị hàm số đã cho không có tiệm cận ngang. 
Mã đề 000 Trang 2/9 B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang. 
 C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x =-3 . 
 D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y =-3. 
Câu 13. Cho hàm số y f() x có đồ thị trên [ 2;4] như hình vẽ bên. 
 y
 2
 1
 -2 -1 O
 2 4 x
 -1
 -3
Tìm giá trị lớn nhất của hàm số trên . 
 A. 2. B. -3. C. -1. D. 1. 
Câu 14. Cho khối hộp chữ nhật ABCD. A B C D có thể tích V . Mệnh đề nào sau đây đúng? 
 1
 A. V AB.. BC AA . B. V AB.. BC AA . C. V AB.. AC AA . D. V AB.. AC AD . 
 3
Câu 15. Cho hàm số y f() x có limfx ( ) 1và limfx ( ) 1. Khẳng định nào sau đây là khẳng định đúng? 
 x x 
 A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x 1 và x 1. 
 B. Đồ thị hàm số đã cho không có tiệm cận ngang. 
 C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang. 
 D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y 1 và y 1. 
Câu 16. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây? 
 A. y x42 2 x . B. y x422 x . C. y x323 x . D. y x32 3 x . 
Câu 17. Đồ thị hàm số nào dưới đây có dạng như hình bên? 
 3 3 42 42
 A. y x3 x . B. y x 3 x . C. y x2 x . D. y x 2 x . 
Câu 18. Một khối lập phương có độ dài cạnh bằng 5 , thể tích khối lập phương đã cho bằng 
 A. 243. B. 25 . C. 81. D. 125. 
Câu 19. Trong các hình sau, hình nào không là hình đa diện lồi? 
Mã đề 000 Trang 3/9 
 A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4. 
Câu 20. Khối chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? 
 A. 3 . B. 4 . C. 5 . D. 6 . 
 21x 
Câu 21. Tìm giá trị lớn nhất của hàm số y trên đoạn  1;3 . 
 x 5
 5 5 3 1
 A. . B. . C. . D. . 
 8 3 4 5
Câu 22. Giá trị lớn nhất của hàm số y x32 3 x 9 x 5trên 1;5 là. 
 A. 15. B. 6. C. 10. D. 22 . 
 3
Câu 23. Cho hàm số fx có f x x x 14 x , xR. Số điểm cực tiểu của hàm số đã cho là 
 A. 4 . B. 3 . C. 1. D. 2 . 
Câu 24. Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 
 x2 x
 A. y x2 32 x . B. y . C. yx 1. D. y . 
 x2 1 x 1
Câu 25. Cho hàm số y f x có bảng biến thiên như sau: 
 Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là: 
 A. 2. B. 3. C. 4. D. 1. 
Câu 26. Hàm số y x434 x đồng biến trên khoảng 
 A. ; . B. 3; . C. 1; . D. ;0 . 
Câu 27. Cho hàm số y f() x có bảng biến thiên như sau 
 x -∞ -1 2 +∞
 y ' + +
 -
 +∞
 y 4 +∞
 3 -5
 - 
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số bằng 
 A. 2. B. 3 . C. 4. D. 1. 
Câu 28. Cho hàm số y f x liên tục trên đoạn  3;0 và có bảng biến thiên như sau: 
Mã đề 000 Trang 4/9 
 Giá trị lớn nhất của hàm số đã cho trên đoạn bằng 
 A. 3 . B. 2. C. 2 . D. 1. 
Câu 29. Khối đa diện có mười hai mặt đều có số đỉnh, số cạnh, số mặt lần lượt là 
 A. 12, 30, 20 . B. 20 , 30, 12. C. 30, 20 , 12. D. 20 , 12, 30 . 
Câu 30. Hình vẽ bên dưới là đồ thị của hàm số nào ? 
 x 1 21x 23x 25x 
 A. y . B. y . C. y . D. y . 
 x 1 x 1 x 1 x 1
Câu 31. Cho lăng trụ tam giác đều ABC. A B C có cạnh đáy bằng a và cạnh bên bằng a 3 . 
 Thể tích của khối lăng trụ ABC. A B C bằng 
 a3 3a3 a3 3a3
 A. . B. . C. . D. . 
 4 4 8 8
Câu 32. Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật AB a , BC 2 a , SA 2 a , SA vuông góc 
 với mặt phẳng ABCD . Tính thể tích khối chóp tính theo a . 
 8a3 4a3 6a3
 A. . B. . C. . D. 4a3 . 
 3 3 3
Câu 33. Hình đa diện sau có bao nhiêu mặt? 
  3;0
 A. 8 . B. 6 . C. 7 . D. 10 . 
Mã đề 000 Trang 5/9 Câu 34. Cho hàm số y f x . Biết đồ thị hàm số y f x có đồ thị như hình vẽ bên 
 Hàm số g x f 23 x x2 đồng biến trên khoảng nào dưới đây? 
 11 1 1 1
 A. ; . B. ; . C. ; . D. 2; . 
 32 2 3 2
Câu 35. Cho một tấm nhôm hình chữ nhật có chiều dài bằng 10cm và chiều rộng bằng 8cm . Người ta cắt bỏ ở 
 bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm , rồi gập 
 tấm nhôm lại (như hình vẽ) để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn 
 nhất. 
 8 2 21 10 2 7 9 21 9 21
 A. x . B. x . C. x . D. x . 
 3 3 9 3
II. TỰ LUẬN ( 3 điểm ). 
Câu 1. ( 1 điểm ) Tính giá trị lớn nhất và nhỏ nhất của hàm số y x3 12 x 1 trên đoạn  2; 3 . 
Câu 2. ( 1 điểm ) Cho hình chóp S. ABC có đáy là tam giác đều cạnh bằng a , cạnh bên SB vuông góc 
với mặt phẳng ABC , SB 2 a . Tính thể tích khối chóp S. ABC . 
Câu 3. ( 1 điểm ) 
 1
 a) (0,5 điểm )Tìm tất cả giá trị thực của tham số m để hàm số y x32 2 mx 4 x 5 đồng biến 
 3
 trên ; . 
 b) (0,5 điểm ) Cho hàm số y f x có bảng biến thiên như hình dưới đây: 
 11
Tìm giá trị cực đại của hàm số g x f 4 x x2 x 3 3 x 2 8 x trên đoạn 1;3 . 
 33
Mã đề 000 Trang 6/9 ĐÁP ÁN 
 I. TRẮC NGHIỆM 7 ĐIỂM 
Đề
\c 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3
âu 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 
00
0 C C B C D D A B D B D D A A D A A D B B A C D D B B A A B B B B C C D 
M
ã 
đề 
00
1 B D C B B C A D B A C A A D B C B A C B B B C B C D C D D B D C B A D 
M
ã 
đề 
00
2 A A D C C A C C A C A D C D B B A A D D D D C B C C C A B A B A C B A 
M
ã 
đề 
00
3 A C A A C C B A A B D B B A B A C C B A A B B B B A D D A B B D A C A 
M
ã 
đề 
00
4 B A B B B C B A D A B B D A B C A D D D D B C A D D B D A D A C D C D 
M
ã 
đề 
00
5 A B B A A A C A C D A C B B D C B B C C D D B B C C A C B A C A A A D 
M
ã 
đề 
00 y x3 12 x 1  2; 3
6 A D A D A D D C C C C SA. ABCB C C A D C A A A A C D D aC B B D SBC B D B A C 
 ABC SB 2 a II. TỰ LUẬN 3 SĐI. ABCỂM 
Câu1 . ( 1 điểm )Tính giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn . 
 Lời giải Điểm 
 Hàm số liên tục trên đoạn 0,25 điểm 
 Ta có: y f( x ) x3 12 x 1. 
 yx 32 12 
 x 2 0,25 điểm 
 y 0 
 x 2
 f( 2) 17; f (2) 15; f (3) 8. 0,5 điểm 
 maxy f ( 2) 17; min y f (2) 15 
  2;3  2;3
 . 
Câu 2 . ( 1 điểm )Cho hình chóp có đáy là tam giác đều cạnh bằng , cạnh bên vuông góc 
với mặt phẳng , . Tính thể tích khối chóp . 
Mã đề 000 Trang 7/9 Lời giải 
 Lời giải Điểm 
 S
 2a
 a
 B C
 A
+) Hình chóp S. ABC có cạnh bên vuông góc với mặt phẳng đáy ABC nên là 0,25 điểm 
 chiều cao của khối chóp S. ABC 
 1 0,25 điểm 
 +) Tính diện tích đáy S . AB . AC sin 600 
 ABC 2
 Ta có thể tích V của khối chóp là : 0,25 điểm 
 1
 V .. S SB 
 3 ABC
 13a2 a3 3 0,25 điểm 
 . .2a . (dvtt). 
 34 6
 SB
Câu 3 . ( 0,25 điểm ) 
a)Tìm tất cả giá trị thực của tham số để hàm số đồng biến trên 
 1
 Lời giải m y x32 2 mx 4 x 5Điểm 
 Tập xác định: DR . 3 0,25 điểm 
 ; y x2 44 mx . 
 Hàm số đã cho đồng biếny ftrên x ; 
 y' 0;  x R 
 4m2 4 0 11 m 0,25 điểm 
 Với m  1;1thì hàm số y x32 x mx 1 đồng biến trên . 
b)Cho hàm số có bảng biến thiên như hình dưới đây: 
Mã đề 000 Trang 8/9 
 Tìm giá trị cực đại của hàm số trên đoạn . 
 Lời giải Điểm 
 Ta có: g x 4 2 x f 4 x x22 x 6 x 8 0,25 điểm 
 2 2 x f 4 x x2 x 4 x 2 
 2
 2 x 2 f 4 x x 4 x . 
 Ta thấy 3 4xx 2 4 ,  x 1;3 f 40 x x2 . 
 Hơn nữa, 4 xx 0,   1;3 . 
 Suy ra 2f 4 x x2 4 x 0 . 
 Do đó, g x 02 x 0,25 điểm 
 Bảng biến thiên 
 Vậy maxg x g 2 f 4 7 0 7 7 . 
 1;3
 Vậy giá trị cực đại của hàm số cần tìm bằng 7 
 11
 g x f 4 x x2 x 3 3 x 2 8 x 1;3
 33
Mã đề 000 Trang 9/9