Đề kiểm tra môn Toán Lớp 12 - Học kỳ I - Năm học 2019-2020 - Trường THPT Hương Khê - Mã đề 003 (Kèm đáp án)

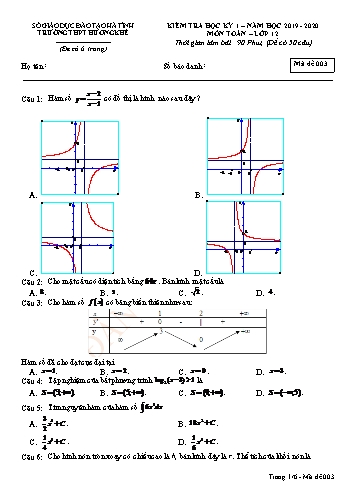
 SỞ GIÁO DỤC ĐÀO TẠO HÀ TĨNH KIỂM TRA HỌC KỲ 1 – NĂM HỌC 2019 - 2020
 TRƯỜNG THPT HƯƠNG KHÊ MÔN TOÁN – LỚP 12
 Thời gian làm bài : 90 Phút; (Đề có 50 câu)
 (Đề có 6 trang)
Họ tên : ............................................................... Số báo danh : ................... Mã đề 003
 x 2
Câu 1: Hàm số y có đồ thị là hình nào sau đây ?
 x 1
 y
 y
 3
 2
 1 1
 -2 -1 0
 1 x -2 -1 0 1 x
 A. B. 
 y
 y
 2
 1
 1
 -2 -1 0 1 x
 -2 -1 0 1 x
 C. D. 
Câu 2: Cho mặt cầu có diện tích bằng 64 . Bán kính mặt cầu là 
 A. 8 . B. 2 . C. 2 . D. 4 . 
Câu 3: Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại
 A. x 1. B. x 2 . C. x 0 . D. x 3 . 
Câu 4: Tập nghiệm của bất phương trình log2 (x 3) 1 là
 A. S (3; ) . B. S (5; ). C. S (4; ) . D. S ( ;5).
Câu 5: Tìm nguyên hàm của hàm số 6x3dx
 3
 A. x4 C . B. 18x2 C . 
 2 
 1 1
 C. x4 C . D. x4 C .
 4 6
Câu 6: Cho hình nón tròn xoay có chiều cao là h, bán kính đáy là r. Thể tích của khối nón là
 Trang 1/6 - Mã đề 003 x x x
 5 2 x
 A. y . B. y . C. y . D. y (0,3) . 
 6 e 3 
Câu 19: Trong các mệnh đề sau, mệnh đề nào đúng?
 A. Mọi hình đa diện luôn có số cạnh gấp hai lần số đỉnh.
 B. Số đỉnh của mọi hình đa diện luôn lớn hơn 4.
 C. Tồn tại một hình đa diện có số cạnh bằng 6.
 D. Số đỉnh và số mặt của mọi hình đa diện luôn luôn bằng nhau.
Câu 20: Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào?
 y
 O 1 2 3
 x
 -2
 -4
 A. y x4 2x2 2 . B. y x3 3x2 .
 C. y x3 3x 2 . D. y x4 2x2 1. 
Câu 21: Cho hàm số y x4 2x2 2 (C) và Parabol (P) : y x2 1. Số giao điểm của (C) và (P) là
 A. 4 . B. 1. C. 3 . D. 2 . 
 x2 x 18 4x 10
 1 1 
Câu 22: Tập nghiệm của bất phương trình 
 5 5 
 A. T ( ; 7][4; ) . B. T [-7;4]. 
 C. T [-4;7] . D. T ( ; 4][7; ) . 
Câu 23: Đạo hàm của hàm số y 1 x 2 là
 2 1 2 1
 A. y ' x 2 1 x . B. y ' 1 x . 
 2 1 2 1
 C. y ' 2 1 x . D. y ' 2 1 x . 
 x 2 
Câu 24: Với giá trị nào của thì biểu thức f (x) log2 x (x 3) xác định.
 x 0 x 3
 A. . B. 3 x 0 . C. x 3. D. . 
 x 3 x 0
Câu 25: Đạo hàm của hàm số y ln(x2 4x) là
 2x 4 2x 4
 A. y ' . B. y ' .
 (x2 4x)2 x2 4x
 2x 4 1
 C. y ' . D. y ' . 
 (x2 4x)ln 2 x2 4x
Câu 26: Cho hình lập phương có diện tích đáy bằng 196a2 . Thể tích khối cầu tiếp xúc với 6 mặt 
của hình lập phương là
 3 3
 1372 a 196 a 3
 A. 1372 a3 . B. . C. . D. 196 a . 
 3 3
 Trang 3/6 - Mã đề 003 2x 1
Câu 36: Cho (C) là đồ thị hàm số y và đường thẳng d : y x m. Có bao nhiêu giá trị 
 x 1 
nguyên m ( 3;7) để đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt? 
 A. 6 B. 3 C. 4 . D. 5 
 x 1
Câu 37: Biết dx a ln x 1 bln x 2 C (a,b ¡ ).Tính giá trị biểu thức P 2a b
 (x 1)(x 2)
 A. 2a b 5. B. 2a b 7. C. 2a b 1. D. 2a b 5. 
Câu 38: Cho hình nón tròn xoay có chiều cao h = 20cm, bán kính đáy r = 25cm. Một thiết diện đi 
qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính 
diện tích của thiết diện đó.
 A. S = 500 cm2 . B. S = 300 cm2 . C. S = 400 cm2 . D. S = 406 cm2 .
Câu 39: Cho hình lăng trụ ABCD.A'B'C 'D' có hình chiếu A' lên ABCD là trung điểm AB , ABCD 
 ¼ 0 0
là hình thoi cạnh 2a, góc ABC 60 , BB ' tạo với đáy một góc 30 . Tính thể tích hình lăng trụ 
ABCD.A'B'C 'D' . 
 2a3
 A. a3 3. B. 2a3. C. a3. D. . 
 3
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên 
mặt phẳng ABCD là trung điểm H của AB , tam giác SAB vuông cân tại S . Biết SH a,CH 3a. 
Tính khoảng cách giữa hai đường thẳng SD và CH.
 2 22a 2 15a 2 18a 14a
 A. . B. . C. . D. . 
 11 3 3 2
 x x 1
Câu 41: Phương trình 9 3 2 0 có hai nghiệm x1, x2 với x1 x2 . Đặt P 2x1 3x2 . Khi đó:
 A. P 2log3 2. B. P 3log3 2. C. P 3log2 3. D. P 0. 
Câu 42: Cho a log2 5 và b log2 3 . Tính giá trị của biểu thức P log3 675 theo a,b.
 2a 2a a 2a b
 A. 3. B. . C. P 3. D. P . 
 b b b b
 x2 4
Câu 43: Đồ thị hàm số y có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
 x2 x 12
 A. 4. B. 2 C. 1. D. 3. 
 1 9
Câu 44: Cho chuyển động thẳng xác định bởi phương trình S t 4 t 2 3t 4 , trong đó t tính 
 4 2
bằng giây (s) và S tính bằng mét (m). Tại thời điểm nào vận tốc của chuyển động đạt giá trị lớn nhất 
?
 A. t 1. B. t 3. C. t 2. D. t 2. 
 1
Câu 45: Cho hàm số y x3 (m 1)x2 mx 2 . Tìm m để hàm số đạt cực đại tại x 1 
 3
 A. không có m. B. m 2 . C. m 1. D. m 1. 
Câu 46: Tất cả các giá trị thực của tham số m để đường thẳng d : y 2x m cắt đồ thị hàm số 
 Trang 5/6 - Mã đề 003