Đề ôn tập cuối học kì I Toán 12 - Đề 4

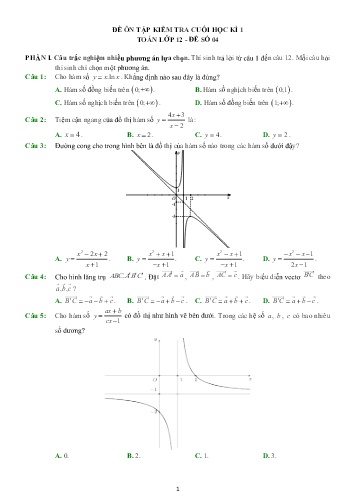
 ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ 1 
 TOÁN LỚP 12 - ĐỀ SỐ 04 
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi 
 thí sinh chỉ chọn một phương án. 
Câu 1: Cho hàm số y= x.ln x . Khẳng định nào sau đây là đúng? 
 A. Hàm số đồng biến trên (0; + ). B. Hàm số nghịch biến trên (0;1) . 
 C. Hàm số nghịch biến trên (0; + ). D. Hàm số đồng biến trên (1; + ). 
 43x +
Câu 2: Tiệm cận ngang của đồ thị hàm số y = là: 
 x − 2
 A. x = 4 . B. x = 2 . C. y = 4 . D. y = 2 . 
Câu 3: Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đậy? 
 y
 1
 O 1 2 x
 -1
 -3
 xx2 −+22 xx2 ++1 xx2 −+1 −xx2 − −1
 A. y = . B. y = . C. y = . D. y = . 
 x +1 −+x 1 −+x 1 21x −
Câu 4: Cho hình lăng trụ ABC. A B C . Đặt AA = a , AB= b , AC= c . Hãy biểu diễn vectơ BC theo 
 abc,, ? 
 A. B' C= − a − b + c . B. B' C= − a + b − c . C. B' C= a + b + c . D. B' C= a + b − c . 
 ax+ b
Câu 5: Cho hàm số y = có đồ thị như hình vẽ bên dưới. Trong các hệ số a , b , c có bao nhiêu 
 cx −1
 số dương? 
 A. 0. B. 2. C. 1. D. 3. 
 1 Câu 6: Dữ liệu về tốc độ của 100 xe ô tô lưu thông trên một đoạn đường cao tốc vào giờ cao điểm, được 
 trích xuất từ camera của cơ quan cảnh sát giao thông. Hãy tìm khoảng biến thiên của mẫu số liệu 
 (bảng số liệu hình bên dưới). 
 Tốc độ (km/h) 60; 70) 70; 80) 80; 90) 90; 100) 100; 110) 
 Số xe 10 20 35 15 
 A. 50km / h. B. 10km / h . C. 30km / h. D. 110km / h . 
Câu 7: Khảo sát thời gian tự học bài ở nhà của học sinh khối 9 ở trường X, ta thu được bảng sau: 
 Thời gian(phút) 0; 30 30; 60 60; 90 90; 120 120; 150 
 ) ) ) ) )
 Số học sinh 9 10 9 15 7 
 Phương sai của mẫu số liệu ghép nhóm là 
 A. 1602. B. 1601, 64 . C. 1601, 9 . D. 1603 . 
Câu 8: Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G( x) =−0, 035 x2 ( 15 x) , trong đó 
 x là liều lượng thuốc được tiêm cho bệnh nhân (0 x 15) . Tính liều lượng thuốc cần tiêm 
 (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.? 
 A. x = 8. B. x =10 . C. x =15 . D. x = 7 . 
 xx2 ++41
Câu 9: Biết đồ thị hàm số y = có tiện cận xiên là đường thẳng y=+ ax b . Tính ab+ . 
 x − 2
 A. 4 . B. 13. C. 12. D. 7 . 
Câu 10: Trong không gian với hệ tọa độ Oxyz cho hai điểm A(−1;5;3) và M (2;1;− 2) . Tìm tọa độ điểm 
 B biết A đối xứng với qua M . 
 11
 A. B ;3; . B. B(−4;9;8) . C. B(5;3;− 7) . D. B(5;−− 3; 7). 
 22
Câu 11: Cho hình lăng trụ ABC. A B C , M là trung điểm của BB . Khẳng định nào sau đây đúng? 
 1
 A. AM=− AC2 AA . B. AM=+ AB AA . 
 2
 1 3
 C. AM= − AB + AA . D. AM=+2 AB AA . 
 2 2
Câu 12: Trong không gian với hệ trục tọa độ Oxyz , cho hình vẽ bên dưới với điểm B (5;4;4) . Hãy xác 
 định tọa độ vectơ AC . 
 A. AC =−(5; 4;4) . B. AC = (5;4;4) . C. AC =−( 5;4;0) . D. AC =( −5;4; − 4) . 
 2 PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi 
 câu, thí sinh chọn đúng hoặc sai. 
 4
Câu 1: Cho hàm số yx=+ . 
 x
 4
 a) Đạo hàm của hàm số đã cho là y =+1 . 
 x2
 b) Đạo hàm của hàm số đã cho nhận giá trị âm trên các khoảng (−2;0) ( 0;2) và nhận giá trị 
 dương trên các khoảng (− ; − 2) ( 2; + ) . 
 c) Bảng biến thiên của hàm số đã cho là: 
 d) Đồ thị hàm số đã cho như ở hình 4: 
 . 
Câu 2: Cho hàm số y= x32 −3 x − 9 x + 1. Xét tính đúng sai của các khẳng định sau: 
 a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1. 
 b) Hàm số nghịch biến trên khoảng (4;7) . 
 c) Hàm số đạt giá trị lớn nhất trên đoạn −2;3 bằng −1. 
 d) Số cực trị của hàm số y= x32 −3 x − 9 x + 1 là 5. 
 3 Câu 3: Hai khinh khí cầu bay lên từ cùng một địa điểm. Sau 30 phút, chiếc thứ nhất cách điểm xuất phát 
 3 km về phía nam và 1,5 km về phía đông, đồng thời cách mặt đất 0,8 km. Chiếc thứ hai nằm 
 cách điểm xuất phát 2 km về phía bắc và 2 km về phía tây, đồng thời cách mặt đất 0,4 km . Giả 
 sử khinh khí cầu chuyển động theo đường thẳng với vận tốc không đổi. 
 Chọn hệ trục Oxyz với gốc O đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng (Oxy) 
 trùng với mặt đất với trục Ox hướng về phía nam, trục Oy hướng về phía đông và trục Oz 
 hướng thẳng đứng lên trời (Hình bên dưới), đơn vị đo lấy theo kilomet. 
 a) Với hệ tọa độ đã chọn, tọa độ khinh khí cầu thứ nhất sau 30 phút là (3; 1,5; 0,8). 
 b) Quãng đường khinh khí cầu thứ nhất đi được sau 30 phút là 3,44 km (Kết quả làm tròn đến 
 chữ số thập phân thứ hai). 
 c) Quãng đường khinh khí cầu thứ hai đi được sau 30 phút là 2,86 km (Kết quả làm tròn đến chữ 
 số thập phân thứ hai). 
 d) Khoảng cách giữa hai khinh khí cầu sau khi đi được 30 phút là 6,11 km (Kết quả làm tròn đến 
 chữ số thập phân thứ hai). 
Câu 4: Thời gian hoàn thành bài kiểm tra môn Toán của các học sinh lớp 12A và 12B được ghi lại ở 
 bảng sau: 
 Thời gian (phút) [25; 30) [30; 35) [35; 40) [40; 45) 
 Số học sinh lớp 12A 7 16 15 4 
 Số học sinh lớp 12B 5 14 17 6 
 a) Khoảng biến thiên cho thời gian hoàn thành bài kiểm tra môn Toán của học sinh mỗi lớp là 
 20 . 
 b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian hoàn thành bài kiểm tra môn Toán 
 của học sinh lớp 12A là 7,78 (kết quả làm tròn đến hàng phần trăm). 
 c) Phương sai của mẫu số liệu ghép nhóm về thời gian hoàn thành bài kiểm tra môn Toán của 
 học sinh lớp 12B là 19,22 (kết quả làm tròn đến hàng phần trăm). 
 d) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh lớp 12A có tốc độ 
 hoàn thành bài kiểm tra môn Toán đồng đều hơn lớp 12B. 
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. 
 4 Câu 1: Trong không gian Oxyz , cho hai điểm AB(3;− 1;2,) ( 1;2;3) . Tọa độ giao điểm E( a;; b c) của 
 đường thẳng AB với mặt phẳng toạ độ (Oxy) . Tính 2abc++ 
Câu 2: Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên. 
 Tìm khoảng tứ phân vị của số liệu đó. (kết quả làm tròn đến hàng phần trăm) 
Câu 3: Cho hình hộp ABCD. A B C D . Giả sử điểm M thuộc AC , điểm N thuộc DC và 
 AM== xAC, DN yDC , đặt BA= a,, BC = b BB = c . Có một cặp ( xy; ) sao cho MN BD , 
 khi đó tính biểu thức T=+ x y 
Câu 4: Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng (Oxy) là mặt nước, trục Oz 
 hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước 2,5m , cách 
 mặt phẳng (Oxz), ( Oyz) lần lượt là 5m và 3m phóng thẳng xuống vị trí con cá, biết con cá cách 
 mặt nước 90cm và cách mặt phẳng (Oxz), ( Oyz) lần lượt là 4m và 3,5 m . Biết tọa độ điểm 
 B( x;; y z) là lúc chim bói cá vừa tiếp xúc với mặt nước. Tính tổng x++ y z (kết quả lấy tròn đến 
 hàng phần trăm). 
Câu 5: Gọi A , B là hai điểm cực trị của đồ thị hàm số f( x) =e2xx − 5e + 2 x + 1. Tính diện tích của tam 
 giác OAB . Kết quả làm tròn đến hàng phần trăm. 
Câu 6: Những căn nhà gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác 
 OAB. O A B như trong Hình 2. Với hệ trục toạ độ Oxyz thể hiện như Hình 2 (đơn vị đo lấy theo 
 5 centimét), hai điểm A và B có tọa độ lần lượt là (240;450;0) và (120;450;300) . Mỗi căn nhà 
gỗ có chiều dài là a cm , chiều rộng là b cm, mỗi cạnh bên của mặt tiền có độ dài là c cm . Tính 
abc++ (Làm tròn đến hàng đơn vị). 
 ---------- HẾT ---------- 
 6