Đề thi thử môn Toán - Kỳ thi thử tốt nghiệp THPT năm 2021 - Trường THPT Nguyễn Trung Thiên - Mã đề 001 (Kèm đáp án)

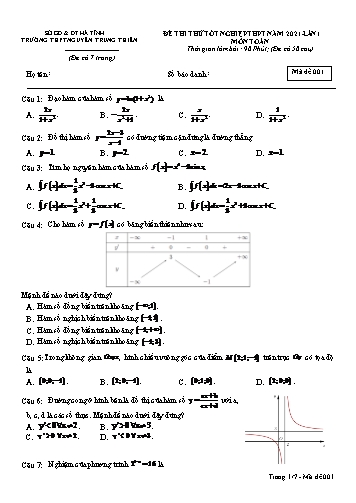
 SỞ GD & ĐT HÀ TĨNH ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2021-LẦN 1
TRƯỜNG THPT NGUYỄN TRUNG THIÊN MÔN TOÁN
 Thời gian làm bài : 90 Phút; (Đề có 50 câu)
 (Đề có 7 trang)
 Họ tên : ............................................................... Số báo danh : ................ Mã đề 001
Câu 1: Đạo hàm của hàm số y ln(1 x2 ) là
 2x 2x x 1
 A. . B. . C. . D. . 
 1 x2 x2 1 1 x2 1 x2
 2x 3
Câu 2: Đồ thị hàm số y có đường tiệm cận đứng là đường thẳng
 x 1
 A. y 1. B. y 2. C. x 2. D. x 1. 
Câu 3: Tìm họ nguyên hàm của hàm số f x x2 3sin x.
 1
 A. f x dx x3 3cos x C. B. f x dx 2x 3cos x C. 
 3 
 1 1 1
 C. f x dx x3 cos x C. D. f x dx x3 3cos x C. 
 3 3 3
Câu 4: Cho hàm số y f x có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
 A. Hàm số đồng biến trên khoảng ;1 .
 B. Hàm số nghịch biến trên khoảng 1;1 . 
 C. Hàm số đồng biến trên khoảng 1; .
 D. Hàm số nghịch biến trên khoảng 1; 3 . 
Câu 5:Trong không gian Oxyz , hình chiếu vuông góc của điểm M 2;1; 1 trên trục Oy có tọa độ 
 là
 A. 0;0; 1 . B. 2;0; 1 . C. 0;1;0 . D. 2;0;0 . 
 ax b
Câu 6: Đường cong ở hình bên là đồ thị của hàm số y với a, 
 cx d
 b, c, d là các số thực. Mệnh đề nào dưới đây đúng?
 A. y ' 0 x 2 . B. y ' 0 x 3.
 C. y ' 0 x 2 . D. y ' 0 x 3 .
Câu 7: Nghiệm của phương trình 21 x 16 là
 Trang 1/7 - Mã đề 001 A. 3. B. 0. C. 1. D. 2. 
Câu 15: Số cạnh của một hình tứ diện là
 A. 12. B. 4. C. 8. D. 6. 
Câu 16: Cho hình trụ có bán kính R = a, mặt phẳng qua trục và cắt hình trụ theo một thiết diện có 
 diện tích bằng 6a2 . Diện tích xung quanh của hình trụ là
 A. 8 a2 B. 6 a2 . C. 8 a3 . D. 6 a . 
Câu 17: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S : (x 3)2 (y 2)2 (z 4)2 25 . 
 Tìm tọa độ tâm I và tính bán kính R của mặt cầu S .
 A. I 3; 2;4 , R 25 . B. I 3;2; 4 , R 25 .
 C. I 3;2; 4 , R 5. D. I 3; 2;4 , R 5. 
Câu 18: Cho hàm số y x3 3x2 2 . Đồ thị của hàm số có điểm cực đại là
 A. 0; 2 . B. 0;2 . C. 2; 2 . D. 2;2 . 
Câu 19: Giá trị lớn nhất của hàm số f x x3 3x trên đoạn [ 3;3] bằng
 A. 18 . B. 2 . C. 18. D. 2 . 
Câu 20: Số giao điểm của đồ thị các hàm số y = x 3 - x với trục hoành là
 A. 1. B. 2. C. 0. D. 3.
Câu 21: Cho F(x) là nguyên hàm của hàm số f (x) 3x2 2x thỏa mãn F(0) 1. Tính F(1)? 
 A. F 1 1. B. F 1 1. C. F 1 2. D. F 1 2.
Câu 22: Cho các số thực dương a,b thỏa mãn 3loga 2logb 1. Mệnh đề nào sau đây đúng?
 A. a3b2 10. B. a3 b2 10. C. 3a 2b 10. D. a3 b2 1. 
Câu 23: Cho hàm số y f x có bảng biến thiên như hình vẽ sau.
 x 1 0 1 
 y 0 + 0 0 +
 y 2 
 1 1
Tìm tất cả các giá trị thực của tham số m để phương trình f x m 0 có 4 nghiệm phân biệt.
 A. m 1;2 . B. m 1;2 . C. m 1;2. D. m 1;2 . 
 2 2
Câu 24: Khi đặt t log2 x , phương trình log2 x 2log4 x 2 0 trở thành phương trình nào sau đây?
 A. 4t 2 t 2 0 . B. 2t 2 t 2 0 . C. t 2 4t 2 0 . D. 2t 2 2t 1 0 . 
Câu 25: Số nghiệm nguyên của của bất phương trình log 1 x 2 2 là
 2
 A. 5. B. 10. C. 4. D. 6. 
Câu 26: Cho a,b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số 
 y loga x, y logb x, y logc x .
 Trang 3/7 - Mã đề 001 1 7 1
 A. m . B. m . C. m 1. D. m . 
 2 4 2
 ax 1
 Câu 33: Cho hàm số f x a,b,c ¡ có bảng biến thiên như sau:
 bx c
 x – ∞ 2 +∞ 
 f'(x) + + ∞
 +∞ 1
 f(x) ∞
 1 – ∞
 Trong các số a,b và c có bao nhiêu số dương?
 A. 0. B. 3. C. 1. D. 2. 
Câu 34: Trong đợt tham quan thực tế, một Đoàn trường THPT cử 30 đoàn viên xuất sắc của 3 khối 
 tham gia. Khối 12 có 6 nam và 4 nữ, khối 11 có 5 nam và 5 nữ, khối 10 có 4 nam và 6 nữ. Chọn 
 mỗi khối 1 đoàn viên làm nhóm trưởng, tính xác suất để trong 3 em làm nhóm trưởng có cả nam 
 và nữ.
 5 19 7 6
 A. . B. . C. . D. . 
 12 25 12 25
Câu 35: Biết rằng đồ thị hàm số y f (x) ax4 bx2 c có hai điểm cực trị là A 0;2 và B 2; 14 . 
 Trong các khẳng định sau khẳng định nào đúng?
 A. f 1 6 . B. f 1 5 . C. f 1 0. D. f 1 7 . 
Câu 36: Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình 
 m.9x 2m 1 .6x m.4x 0 nghiệm đúng với mọi x 0;1 ?
 A. 5. B. Vô số. C. 8. D. 6.
Câu 37: Cho hình nón N có đáy là hình tròn tâm O , đỉnh S , thiết diện qua trục là tam giác đều 
 cạnh 2a. Cho điểm H thay đổi trên đoạn thẳng SO . Mặt phẳng P vuông góc với SO tại H và 
 cắt hình nón theo đường tròn C .Khối nón có đỉnh O và đáy là hình tròn C có thể tích lớn nhất 
 bằng bao nhiêu?
 4 3 a3 2 3 a3 3 3 a3 3 a3
 A. . B. . C. . D. . 
 81 81 81 81
 2x 1 2 18 19 
Câu 38: Cho hàm số f (x) x . Tổng f (0) f f ... f f bằng
 2 2 10 10 10 10 
 19 59 28
 A. . B. . C. 10. D. .
 2 6 3
Câu 39: Một kĩ sư mới ra trường làm việc với mức lương khởi điểm là 7.000.000 đồng/tháng. Cứ 
 sau 9 tháng làm việc, mức lương của kĩ sư đó lại được tăng thêm 10% . Hỏi sau 4 năm làm việc, 
 tổng số tiền lương kĩ sư đó nhận được là bao nhiêu?
 A. 407.721.300 đồng. B. 418.442.010 đồng.
 C. 421.824.081 đồng. D. 415.367.400 đồng. 
 Trang 5/7 - Mã đề 001 A. 66. B. 63. C. 65. D. 64.
Câu 46: Cho hàm số y f x có bảng biến thiên sau:
 x -2 3 
 y 0 + 0
 5
 y
 16 
 1 5 7
Tìm giá trị nhỏ nhất của hàm số g x f x3 3x x5 x3 4x trên đoạn  1;2?
 5 3 15
 A. 19. B. 20. C. 21. D. 22 .
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt thuộc các 
 AB AD
 đoạn thẳng AB, AD ( M , N không trùng A ) sao cho 2 4 . Ký hiệu V ,V lần lượt là thể 
 AM AN 1
 V
 tích của các khối chóp S.ABCD và S.MBCDN . Giá trị lớn nhất của tỷ số 1 bằng
 V
 1 2 4 3
 A. . B. . C. . D. . 
 6 3 7 4
Câu 48: Cho hàm số y f x xác định và có đạo hàm trên ¡ và thỏa mãn 
 2 f (2x) f (1 2x) 12x2. Phương trình tiếp tuyến của đồ thị hàm số y f x tại điểm có hoành 
 độ bằng 1 tạo với hai trục Ox,Oy một tam giác có diện tích S bằng
 1 3
 A. S 1. B. S . C. S 2. D. S .
 2 2
Câu 49: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AB BC 5a ; 
 9
 SA  AB, SC  BC . Biết góc giữa hai mặt phẳng SBC và SBA bằng với cos . Thể tích 
 16
 của khối chóp S.ABC là
 50a3 125 7a3 50a3 125 7a3
 A. . B. . C. . D. . 
 3 18 9 9
Câu 50: Cho hàm số y = f (x) liên tục trên R và có đồ thị như hình vẽ. Hỏi 
 m3 + 4m
 có bao nhiêu số nguyên dương m để phương trình = f 2 (x)+ 2 
 8 f 2 (x)+ 1
 có 4 nghiệm phân biệt thuộc đoạn [-2;6]?
 A. 1. B. 2. C. 4. D. 3. 
 ------ HẾT ------
 Trang 7/7 - Mã đề 001