Đề thi thử tốt nghiệp THPT môn Toán Lớp 12 - Trường THPT Hương Sơn - Mã đề 004

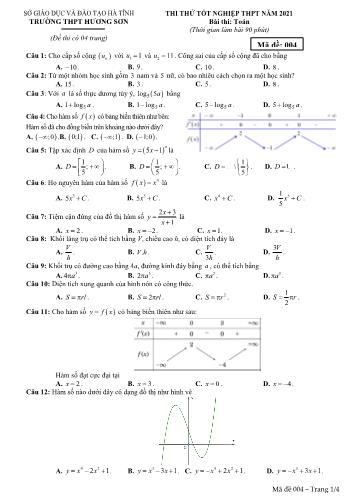
 SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ TĨNH THI THỬ TỐT NGHIỆP THPT NĂM 2021 
 TRƯỜNG THPT HƯƠNG SƠN Bài thi: Toán 
 (Thời gian làm bài 90 phút) 
 (Đề thi có 04 trang) 
 Mã đề: 004 
 Câu 1: Cho cấp số cộng un với u1 1 và u2 11. Công sai của cấp số cộng đã cho bằng 
 A. 10 . B. 9 . C. 10. D. 8 . 
 Câu 2: Từ một nhóm học sinh gồm 3 nam và 5 nữ, có bao nhiêu cách chọn ra một học sinh? 
 A. 15. B. 3 . C. 5 . D. 8 . 
 Câu 3: Với a là số thực dương tùy ý, log55 a bằng 
 A. 1log 5 a . B. 1log 5 a . C. 5log 5 a . D. 5log 5 a . 
 Câu 4: Cho hàm số fx có bảng biến thiên như bên: 
 Hàm số đã cho đồng biến trên khoảng nào dưới đây? 
 A. ;0 .B. 0;1 . C. ;1 . D. 1;0 . 
 π
 Câu 5: Tập xác định D của hàm số yx 51 là 
 1 1 1
 A. D ; . B. D ; . C. D \ . D. D . 
 5 5 5
 Câu 6: Họ nguyên hàm của hàm số f xx 4 là 
 1
 A. 5xC3 . B. 5xC5 . C. xC4 . D. xC5 . 
 5
 23x 
 Câu 7: Tiệm cận đứng của đồ thị hàm số y là 
 x 1
 A. x 2 . B. x 2. C. x 1. D. x 1. 
 Câu 8: Khối lăng trụ có thể tích bằng V, chiều cao h, có diện tích đáy là 
 V V 3V
 A. . B. Vh. . C. . D. . 
 h 3h h
 Câu 9: Khối trụ có đường cao bằng 4a, đường kính đáy bằng a , có thể tích bằng 
 A. 4 a3 . B. 2 a3 . C. a2 . D. a3 . 
 Câu 10: Diện tích xung quanh của hình nón có công thức. 
 1
 A. Srl . B. Srl 2 . C. Sr 2 . D. Sr . 
 2
 Câu 11: Cho hàm số y f x có bảng biến thiên như sau: 
 Hàm số đạt cực đại tại 
 A. x 2 . B. x 3. C. x 0 . D. x 4. 
 Câu 12: Hàm số nào dưới đây có dạng đồ thị như hình vẽ 
 A. y x42 21 x . B. y x3 31 x . C. y x42 21 x . D. y x3 31 x . 
 Mã đề 004 – Trang 1/4 2
Câu 28: Phương trình 2425xx 4 có tổng tất cả các nghiệm bằng 
 5 5
 A. . B. 1. C. . D. 1. 
 2 2
 e 3ln1x 
Câu 29: Tính tích phân Idx bằng cách đặt ux 3ln1 . Mệnh đề nào dưới đây đúng? 
 1 x
 3 2 2 2 1 14 2 e
 A. Iu du 2 . B. Iu du 2 . C. Idu . D. Iu du 2 . 
 2 1 3 1 0 9 3 1
Câu 30: Cho hàm số yfx có bảng biến 
thiên như bên. 
Tổng số đường tiệm cận đứng và tiệm cận 
ngang của đồ thị hàm số đã cho là 
 A. 1. B. 4 . C. 3 . D. 2 . 
Câu 31: Trong không gian Oxyz ,cho điểm ABC 1; 2;3 , 0;3;1 , 4;2;2 .Cosin của góc BAC là. 
 9 9 9 9
 A. . B. . C. . D. . 
 35 35 235 235
Câu 32: Một hình nón có diện tích xung quanh bằng 8 và thiết diện qua trục là tam giác đều, có độ dài 
đường sinh là. 
 A. 4 . B. 8. C. 2 . D. 1 . 
Câu 33: Cho khối chóp S. ABC có thể tích bằng 8 . MN, lần lượt là trung điểm của SA, SB . Tính thể tích 
khối chóp S. MNC . 
 A. 4 . B. 2 . C. 8 . D.16. 
Câu 34: Trong hình bên, đường cong là đồ thị của hàm số 
 yx ln , điểm B là trung điểm của đoạn thẳng AC. Khẳng định 
nào sau đây là đúng? 
 A. a c2 b . B. ac b2 . 
 C. ac 2 b2 . D. ac b . 
Câu 35: Trong không gian (Oxyz) , Cho ABCD 2;0;0 , 0;4;0 , 0;0;6 , 2;4;6 . 
 Mặt phẳng P // ABC ; P cách đều điểm D và ABC . Mặt phẳng P có phương trình là. 
 A. 6x 3 y 2 z 10 0. B. 6x 3 y 2 z 36 0. C. 6x 3 y 2 z 24 0 . D. 6x 3 y 2 z 0 . 
 2 dx
Câu 36: Biết aln 2 b ln 3 c ln 5. Khi đó giá trị a 2 b c bằng 
 1 xx 1 2 1 
 A. 3. B. 2 . C. 1. D. 2 . 
Câu 37: Hình bên cho ta hình ảnh của một đồng hồ cát với các kích thước kèm theo, 
 Vn
OA OB . Gọi Vn là tổng thể tích của 2 khối nón, Vt là thể tích khối trụ. Tỉ số bằng 
 Vt
 1 1 1 1
 A. . B. . C. . D. . 
 3 2 6 4
 22
Câu 38: Cho phương trình log (10x ) 2 m log10x x log(10 x ) 0 . Gọi S là tập chứa tất cả các giá trị nguyên của 
 m  10;10  để phương trình đã cho có đúng 3 nghiệm phân biệt. Số phần tử của tập S là 
 A. 20 . B.10. C. 11. D. 19. 
Câu 39: Cho khối lăng trụ ABCABC''' có đáy là tam giác đều cạnh a , cạnh bên AA' a , góc giữa AA' 
 và mặt đáy bằng 300 . Tính thể tích khối lăng trụ đã cho theo a . 
 a3 3 a3 3 a3 3 a3 3
 A. . B. . C. . D. . 
 24 12 8 4
Câu 40: Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số 
thuộc S , xác suất để số đó có hai chữ số tận cùng có cùng tính chẵn lẻ bằng 
 2 4 32 32
 A. . B. . C. . D. . 
 5 9 81 45
 Mã đề 004 – Trang 3/4