Giáo án Giải tích 11 - Tiết 60+62+64 - Năm học 2019-2020

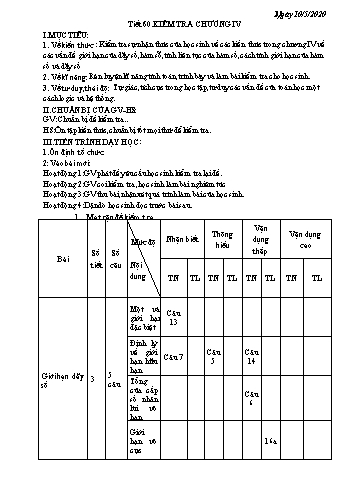
 Ngày 10/5/2020
 Tiết 60.KIỂM TRA CHƯƠNG IV
I.MỤC TIÊU:
1. Về kiến thức : Kiểm tra sự nhận thức của học sinh về các kiến thức trong chương IV về 
các vấn đề giới hạn của dãy số,hàm sỗ,tính liên tục của hàm số,cách tính giới hạn của hàm 
số và dãy số
2. Về kĩ năng:Rèn luyện kĩ năng tính toán,trình bày và làm bài kiểm tra cho học sinh.
3. Về tư duy,thái độ: Tự giác,tích cực trong học tập,tư duy các vấn đề của toán học một 
cách logic và hệ thống.
II.CHUẨN BỊ CỦA GV-HS:
GV: Chuẩn bị đề kiểm tra..
HS:Ôn tập kiến thức,chuẩn bị tốt mọi thứ để kiểm tra. 
III.TIẾN TRÌNH DẠY HỌC:
1.Ổn định tổ chức:
2:Vào bài mới:
Hoạt động 1:GV phát đề yêu cầu học sinh kiểm tra lại đề.
Hoạt động 2:GV coi kiểm tra ,học sinh làm bài nghiêm túc
Hoạt động 3:GV thu bài,nhận xét quá trình làm bài của học sinh.
Hoạt động 4:Dặn dò học sinh đọc trước bài sau.
 1. Ma trận đề kiểm tra
 Vận 
 Thông Vận dụng 
 Nhận biết dụng 
 Mức độ hiểu cao
 Số Số thấp
 Bài
 tiết câu Nội 
 dung TN TL TN TL TN TL TN TL
 Một vài 
 Câu 
 giới hạn 
 13
 đặc biệt
 Định lý 
 về giới Câu Câu 
 Câu 7
 hạn hữu 5 14
 hạn
Giới hạn dãy 5 
 3
số câu Tổng 
 của cấp 
 Câu 
 số nhân 
 6
 lùi vô 
 hạn 
 Giới 
 hạn vô 16a
 cực 1 1 1
Câu 6: Tính tổng: S = 1 + ... 
 3 9 27
 1 3
 A. B. 1 C. D. 2
 2 2
 un
 limun 4
Câu 7: Cho , limvn 2 . Giới hạn lim bằng:
 vn
 A. -4 B. C. D. 2
Câu 8: Trong các mệnh đề sau mệnh đề nào đúng?
A.lim x5 B. lim x2 C. lim x4 D. lim x3 
 x x x x 
 x2 3x 2
Câu 9. lim bằng:
 x 1 x2 x
 5
A. 1 B. C. -1 D. 0
 4
 2x 1
Câu 10. Tìm giới hạn lim ?
 x 2 x 1
A.0 B. 5 C. 1 D. 2
 5x 2khi x 2
 f (x)
Câu 11: Cho hàm số 2 . Tìm giới hạn lim f (x) .
 x 1khi x 2 x 2
A.5 B. 8 C. 3 D. Không tồn tại
 9x2 x 2 a
Câu 12: lim (a;b nguyên). Khi đó a-b bằng: 
 x 4x2 3x 1 b
 9 3
 A. 1 B. C. D.-1
 4 2
Câu 13 . Dãy số nào sau đây có giới hạn bằng 0?
 n n n n
 4 1 5 5 
 A. B. C. D. 
 3 3 3 3 
 4n 2.3n
Câu 14.Tìm giới hạn lim . ta được kết quả :
 2n 3.4n
 1
A. B. - C. -1 D. 1
 3
 x 1 x2 x 1
Câu 15. lbằng:im
 x 0 x
 5
A. 0 B. C. -1 D. 
 4
 1
 A. 2 B. -1 C. 1 D. 
 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
C B A A B C D C C B D A B A A
Phần 2: Tự luận
Câu 16:(3 điểm). Tính các giới hạn sau:
 2
 2n n 1 3 2x 3
 a) lim 2 b) lim (x 2x) c) lim
 4 3n x x 1 x 1
Câu 17: ( 1 điểm). Xét tính liên tục của hàm số sau tại x = 2 Ngày 3/5/2020
 Tiết 62. ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM
 I. Mục tiêu :
 1. Kiến thức: 
 - Học sinh biết được ý nghĩa hình học của đạo hàm.
 - Biết vận dụng công thức để viết phương trình tiếp tuyến của đồ thị hàm số.
 -Nắm vững ý nghĩa hình học và vật lí của đạo hàm.
 -Hiểu rõ mối quan hệ giữa tính liên tục và sự tồn tại đạo hàm.
 2.Kỹ năng: 
 Biết cách tính đạo hàm tại một điểm bằng định nghĩa của các hàm số thường 
 gặp.
 Vận dụng tốt vào viết phương trình tiếp tuyến.
 3.Thái độ:
 Tư duy các vấn đề của toán học một cách lôgic và hệ thống.
 4.Đinh hướng phát triển năng lực:
 - Năng lực hợp tác: Tổ chức nhóm học sinh hợp tác thực hiện các hoạt động.
 - Năng lực tự học, tự nghiên cứu: Học sinh tự giác tìm tòi, lĩnh hội kiến thức và phương 
 pháp giải quyết bài tập và các tình huống.
 - Năng lực giải quyết vấn đề: Học sinh biết cách huy động các kiến thức đã học để giải 
 quyết các câu hỏi. Biết cách giải quyết các tình huống trong giờ học.
 - Năng lực thuyết trình, báo cáo: Phát huy khả năng báo cáo trước tập thể, khả năng thuyết 
 trình.
 II. Chuẩn bị của giáo viên và học sinh
 1. Giáo viên:
 - Thiết kế hoạt động học tập hợp tác cho học sinh tương ứng với các nhiệm vụ cơ bản của 
 bài học. 
 - Tổ chức, hướng dẫn học sinh thảo luận, kết luận vấn đề.
 2. Học sinh:
 - Mỗi học sinh trả lời ý kiến riêng và phiếu học tập. Mỗi nhóm có phiếu trả lời kết luận 
 của nhóm sau khi đã thảo luận và thống nhất.
 - Mỗi cá nhân hiểu và trình bày được kết luận của nhóm bằng cách tự học hoặc nhờ bạn 
 trong nhóm hướng dẫn.
 - Mỗi người có trách nhiệm hướng dẫn lại cho bạn khi bạn có nhu cầu học tập.
 III. Chuỗi các hoạt động học:
 +Mục tiêu:
 - Học sinh biết được ý nghĩa hình học của đạo hàm.
 - Biết vận dụng công thức để viết phương trình tiếp tuyến của đồ thị hàm số.
 * Nội dung, phương thức tổ chức:
+) HĐ1: Khởi động. GỢI Ý
HĐ1.1. Cho đường cong (C) và M0 (C). M là điểm di động trên (C). Vị trí giới hạn M 0T (nếu có) 
của cát tuyến M0M đgl tiếp tuyến của (C) tại M0. Điểm M0 đgl tiếp điểm.
Chỳ ý: Không xét tiếp tuyến song song hoặc trùng với Oy.
b) Ý nghĩa hình học của đạo hàm
Định lí 2: 
 Đạo hàm của y = f(x) (C) tại điểm x 0 là hệ số góc của tiếp tuyến M 0T của (C) tại điểm 
M0(x0; f(x0)).
c) Phương trình tiếp tuyến
Định lý 3: Phương trình tiếp tuyến của (C): y = f(x) tại điểm M0(x0; f(x0)) là
 y – y0 = f (x0).(x – x0)
trong đó y0 = f(x0).
+) HĐ3: Củng cố. GỢI ớ
 HĐ3.1. Tìm hệ số góc của tiếp tuyến HĐ 3.1 : Gọi x là số gia tại điểm x0 = -2, ta có:
của đồ thị hàm số y x2 3x 2tại 
 2
điểm có hoành độ -2. y f ( x 2) f ( 2) ( x 2) 3( x 2) 2 12
 2 x 7 x
 y 2 x 7 x
 Suy ra: lim lim lim x 7 7 
 x 0 x x 0 x x 0
 Vậy, y’(-2) = 7.
 2
HĐ3.2: Cho hàm số y x 3x -2 . HĐ3.2: Gọi M (x0 ; y0 ) là tiếp điểm
Viết pttt của đồ thị hàm số trên tại Ta có x0 2 y0 12 
điểm có hoành độ -2. Hệ số góc tiếp tuyến k=7.
 Vậy phương trình tiếp tuyến y=7(x+2)-12=7x+2.
 Ý NGHĨA VẬT LÍ CỦA ĐẠO HÀM.(10’)
 * Mục tiêu: 
 - Học sinh biết được ý nghĩa vật lí của đạo hàm.
 - Biết vận dụng công thức để tính vận tốc tức thời, cường độ tức thời tại thời điểm 
 t0.
 * Nội dung, phương thức tổ chức:
 +) A. Khởi động. GỢI Ý
 HĐ1.1. Theo định nghĩa
 f (t) f (t )
 V(t ) lim 0 s'(t )
 0 t t 0
 0 t t0
 HĐ1.2. Điện lượng Q = Q (t ) cường độ dòng 
 I (t 0) = Q '(t 0)
 điện I (t 0) = ? 
 +) HĐ2: Hình thành kiến thức. * Từ đó HS đọc đạo hàm bằng định nghĩa đạo hàm của hàm số trên một 
 khoảng
 HÐ1.2.1: Khởi động (Tiếp cận). Gợi ý
 Cho các hàm số sau
 2
 a. y f (x) x tính đạo hàm bằng định nghĩa tại điểm a. y '(x0 ) 2x0
 x0
 b. y '(x ) 0
 b. y c tính đạo hàm bằng định nghĩa tại điểm x0 , với 0
 c là hằng số
 1
 c. y x tính đạo hàm bằng định nghĩa tại điểm x0 0
 c. y'(x0) 
 , 2 x0
+ Thực hiện: Học sinh suy nghĩ và làm ví dụ vào giấy nháp.
 + Báo cáo, thảo luận: Chỉ định một học sinh bất kì trình bày lời giải, các học sinh khác 
thảo luận để hoàn thiện lời giải.
 + Đánh giá, nhận xét, tổng hợp chốt kiến thức: Trên cơ sở câu trả lời của học sinh, giáo 
viên chuẩn hóa lời giải, từ đó nêu định nghĩa và đạo hàm trên một khoảng , quy tắc tính 
đạo hàm của 4 hàm số thường gặp. HS viết bài vào vở.
II.1.Định nghĩa: Đạo hàm trên một khoảng
Hàm số y f (x) được gọi là có đạo hàm trên khoảng (a;b) nếu nó có đạo hàm tại mọi 
điểm x trên khoảng đó.Khi đó, ta gọi hàm số f ' : (a;b) ¡ 
 x f '(x) 
là đạo hàm của hàm số y f (x) trên khoảng (a;b) , kí hiệu là y ' hay f '(x).
 D. CŨNG CỐ
Câu 1: Số gia của hàm số f x 2x 1 ứng với số gia x của đối số x tại x0 5 là:
A. B.9 C. 2 x 4 D. 9 2 x 3 9 2 x 5 9 2 x 1
 y x2 x
Câu 2: Tỉ số của hàm số f x ứng với số gia x của đối số x tại x 1là:
 x x 2 0
 5 x 6 x 5 x 4 x
A. B. C. D. 
 x 1 x 1 x 2 x 1
Câu 3: Phương trình tiếp tuyến của đồ thị hàm số tạif xđiểm xcó2 hoành3x 2 độ 
 x0 2 là:
 A. y x 3 B. y x 1 C. y x 2 D. y x 2
 2x 1
Câu 4: Hệ số góc của tiếp tuyến với đồ thị hàm số f x tại điểm có hoành độ 
 x 4
 x0 2 là:
 9 5 1 7
A. B. C. D. 
 36 36 36 36 Tiết 64. QUY TẮC TÍNH ĐẠO HÀM (3t)
I. MỤC TIÊU
 1. Kiến thức: Học sinh nắm được quy tắc tính đạo hàm của tổng, hiệu, tích , thương 
các hàm số; nắm được các công thức đạo hàm của các hàm số thường gặp. Phải xác định 
được hàm số đã cho thuộc dạng công thức nào?
 2. Kĩ năng: Tìm được đạo hàm của các hàm số thường gặp
 3. Thái độ: Nghiêm túc trong học tập, coi trọng môn học.
 4. Định hướng phát triển năng lực: 
 + Năng lực chung: Tự học; giải quyết vấn đề; sáng tạo; tự quản lý; giao tiếp; hợp tác; 
 sử dụng CNTT; sử dụng ngôn ngữ; tính toán.
 + Năng lực chuyên biệt: Vận dụng các tri thức Toán; giải một số bài toán có tính thực 
 tiễn điển hình; vận dụng tri thức Toán, phương pháp tư duy Toán vào thực tiễn. Giao 
 tiếp, sử dụng ngôn ngữ toán.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH:
 1. Giáo viên:
 - Thiết bị dạy học: thước , phấn.
 - Phiếu học tập của học sinh.
 2. Học sinh:
 - Ôn lại kiến thức về định nghĩa đạo hàm.
 - Bảng phụ.
III. CHUỖI CÁC HOẠT ĐỘNG:
 1. GIỚI THIỆU: 
 Chào các em, về tính đạo hàm bằng định nghĩa nhìn chung là phức tạp. Đối với một số 
 hàm thường gặp ta có các qui tắc và các công thức cho phép ta tính đạo hàm của chúng 
 nhanh hơn. Như vậy các qui tắc và công thức đó là gì? Đó chính là nội dung bài học của 
 chúng ta ngày hôm nay:“Qui tắc tính đạo hàm”
 2. NỘI DUNG BÀI HỌC:
Hoạt động 1: Tiếp cận đạo hàm của các hàm số thường gặp. 
1. Mục tiêu: Nắm bắt được các hàm số thường gặp, cách tính đạo hàm của các hàm số 
thường gặp.
2. Phương pháp/Kĩ thuật dạy học: Phát vấn.
3. Hình thức tổ chức hoạt động: Nêu vấn đề.
4. Phương tiện dạy học:
5. Sản phẩm:
 2
Bài toán 1:Hãy tính đạo hàm của hàm số y f (x) x tại x0 bằng 2.
=> Bài toán này học sinh có thể dự đoán được đạo hàm của hàm số y f (x) x10 đạo hàm dương và tính đạo hàm của hàm số 
 y x tại điểm tại x tùyý.
 1 0
 y’ = x , (x 
 2 x + Gv yêu cầu ba nhóm trình + Hs ghi nhận.
> 0) bày kết quả và đưa ra nhận 
 xét.
Hoạt động 3: Đạo hàm tổng, hiệu, tích, thương. (22p)
1. Mục tiêu: Nắm chắc đạo hàm của tổng ,hiệu, tích, thương.
2. Phương pháp/Kĩ thuật dạy học: dạy học nhóm.
3. Hình thức tổ chức hoạt động: Nhiệm vụ được giao cho cả lớp. HS thực hiện công việc 
theo nhóm.
4. Phương tiện dạy học: bẳng, phấn, thước.
5. Sản phẩm: Bài báo cáo kết quả hoạt động nhóm.
Nội dung kiến thức Hoạt động của GV Hoạt động của HS
Vd4: Giả sử u = u(x), v = v(x) + Gv gợi ý cho hs sử dụng + Hs thực hiện theo nhóm.
là các hàm số có đạo hàm tại định nghĩa để làm vd4. 
điểm x thuộc khoảng xác định. Sau đó học sinh làm việc 
Chứng minh : (u + v)’ = u’ + theo nhóm và giải vd 4.
v’(đọc SGK)
 + Gv yêu cầu 2 nhóm bất + Hs trình bày.
Định lí : Giả sử u = u(x), v = kì lên trình bày. Sau đó 
 + hs lắng nghe và ghi 
v(x) là các hàm số có đạo hàm nhận xét .
 nhận.
tại điểm x thuộc khoảng xác 
 + Gv nêu định lý và chú ý.
định. Ta có: + Hs lắng nghe và nghi 
 nhận.
(u + v)’ = u’ + v’ (1)
(u - v)’ = u’ - v’ (2)
(u.v)’ = u’v + v’u (3)
 '
 u u 'v v 'u
 2 (v v(x) 0) (4)
 v v
 1 v '
+ Chú ý : 2
 v v
+ Có thể mở rộng thêm đạo + Gv ghi ví dụ 5. yêu cầu + Hs làm bài tập theo 
hàm của tổng, hiệu, tích cho hs sử dụng kiến thức đã nhóm.
 học về đạo hàm để giải.( 
u1.u2,..., un
 hs giải theo nhóm hai 
VD 5: Tính đạo hàm của các người)
hàm số sau:
 + Gv yêu cầu 4 nhóm bất 
a) y = 5x3 – 2x5- 3x +4 lỳ lên giải, trình bày cụ thể 
 + Hs thực hiện
 đã sử dụng công thức gì để 
b) y = -x3 x .
 giải sau đó nhận xét bài 
 1 3x giải của học sinh
c) y 
 2x 5