Giáo án Giải tích 12 - Tiết 64: Kiểm tra giữa kì II

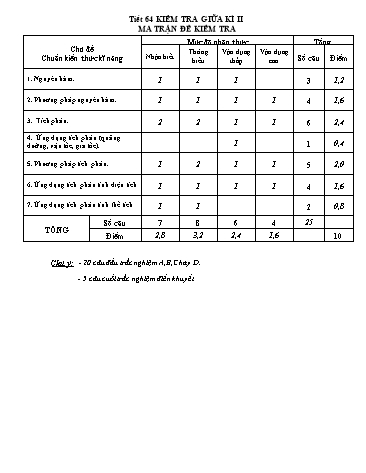
 Tiết 64 KIỂM TRA GIỮA KÌ II
 MA TRẬN ĐỀ KIỂM TRA 
 Mức độ nhận thức Tổng
 Chủ đề
 Thông Vận dụng Vận dụng 
 Chuẩn kiến thức kĩ năng Nhận biết Số câu Điểm
 hiểu thấp cao
1. Nguyên hàm. 1 1 1 3 1,2
2. Phương pháp nguyên hàm. 1 1 1 1 4 1,6
3. Tích phân. 2 2 1 1 6 2,4
4. Ứng dụng tích phân (quảng 
 1 1 0,4
đường, vận tốc, gia tốc).
5. Phương pháp tích phân. 1 2 1 1 5 2,0
6. Ứng dụng tích phân tính diện tích 1 1 1 1 4 1,6
7. Ứng dụng tích phân tính thể tích 1 1 2 0,8
 Số câu 7 8 6 4 25
 TỔNG
 Điểm 2,8 3,2 2,4 1,6 10
 Chú ý: - 20 câu đầu trắc nghiệm A,B,C hay D.
 - 5 câu cuối trắc nghiệm điền khuyết. b b b b b
 A. kf x dx k f x dx . B. f x g x dx f x dx. g x dx .
 a a a a a
 b b b b b b
 C. f x g x dx f x dx g x dx . D. f x g x dx f x dx g x dx .
 a a a a a a
 e ln x
Câu 5: Cho tích phân I dx . Nếu đặt t ln x thì
 1 x
 1 t 1 1 e
 A. I dt B. I t 2 dt C. I t dt D. I t dt
 t 
 0 e 0 0 1
Câu 6: Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y x2 , trục hoành Ox , các đường thẳng x 1, 
x 2 là
 8 7
 A. S . B. S . C. S 8. D. S 7 .
 3 3
Câu 7: Cho hàm số f x cos x . Mệnh đề nào sau đây đúng
 A. f x dx sin x C . B. f x dx cos x C .
 C. f x dx cos x C . D. f x dx sin x C .
Câu 8: Cho hàm y f x liên tục và không âm trên a;b . Tính thể tích khối tròn xoay được tạo thành khi quay 
hình phẳng H được giới hạn bởi các đường y f x , trục Ox và hai đường thẳng x a , x b , a b xung 
quanh trục Ox .
 b b b b
 A. f 2 x dx . B. 2 f 2 x dx . C. f 2 x dx . D. f x dx .
 a a a a
Câu 9: Cho I x2 1 2xdx . Bằng cách đặt t x2 1, khẳng định nào sau đây đúng
 1
 A. I 2 tdt B. I tdt C. I t 1 dt D. I tdt
 2 
Câu 10: Cho hàm số f x liên tục trên a;b . Hãy chọn mệnh đề sai dưới đây:
 b a
 A. f x dx f x dx .
 a b
 b c b
 B. f x dx f x dx f x dx với c a;b .
 a a c e ln x 3
Câu 17: Biết I dx a ln b, a,b Q . Mệnh đề nào sau đây đúng?
 1 x ln x 2 2
 A. a b 1. B. 2a b 1 . C. a 2b 0 . D. a2 b2 4 .
Câu 18: Gọi F x là một nguyên hàm của hàm số f x xe x . Tính F x biết F 0 1.
 A. F x x 1 e x 2 . B. F x x 1 e x 2 .
 C. F x x 1 e x 1. D. F x x 1 e x 1.
 1
Câu 19: Biết F x là một nguyên hàm của f x và F 0 2 thì F 1 bằng.
 x 1
 A. ln 2 . B. 3 . C. 4 . D. 2 ln 2 .
 2 1 a a
Câu 20: Giả sử dx ln với a , b ¥ * và tối giản. Tính M a2 b2 .
 1 2x 1 b b
 A. M 28 . B. M 34 . C. M 14 . D. M 8 .
 Phần II: Câu hỏi trắc nghiệm điền khuyết.
Câu 21: Tính diện tích S của hình phẳng giới hạn bởi hai đồ thị hàm số y 2x2 và y 5x 2 .
Câu 22: Biết F x là một nguyên hàm của hàm f x x ln x 1 và F 0 0, F 2 a ln b với a,b ¤ . 
Tính P a b. 
 1
Câu 23: Cho hàm số f x có đạo hàm liên tục trên đoạn 0;1 và thỏa mãn f 0 6, 2x 2 . f x dx 6 . 
 0
 1
Tích phân f x dx .
 0
Câu 24: Cho hàm số y = f (x) có đạo hàm liên tục trên [- 2;4]. Đồ thị của
 hàm số y = f ¢(x) được cho như hình bên. Diện tích hình phẳng giới hạn 
bởi trục Ox và đồ thị hàm số y = f ¢(x) trên đoạn [- 2;1] và [1;4] lần lượt 
bằng 9 và 12. Cho f (1)= 3. Tính tổng f (- 2)+ f (4).
 1 2
Câu 25: Cho hàm số f x thỏa mãn f 2 , f x x3 f x và f x 0 với mọi x ¡ . Tính giá trị 
 5 
của f 1 . 
 ----------- HẾT ----------