Giáo án môn Toán Lớp 12 - Tiết 58-64, Chủ đề: Số phức

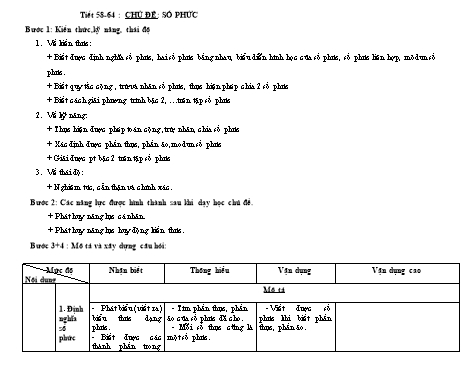
 Tiết 58-64 : CHỦ ĐỀ: SỐ PHỨC 
Bước 1: Kiến thức,kỹ năng, thái độ
 1. Về kiến thức:
 + Biết được định nghĩa số phức, hai số phức bằng nhau, biểu diễn hình học của số phức, số phức liên hợp, môdun số 
 phức. 
 + Biết quy tắc cộng , trừ và nhân số phức, thực hiện phép chia 2 số phức
 + Biết cách giải phương trình bậc 2, trên tập số phức
 2. Về kỹ năng:
 + Thực hiện được phép toán cộng ,trừ, nhân, chia số phức
 + Xác định được phần thực, phần ảo,modun số phức
 + Giải được pt bậc 2 trên tập số phức
 3. Về thái độ:
 + Nghiêm túc, cẩn thận và chính xác.
 Bước 2: Các năng lực được hình thành sau khi dạy học chủ đề.
 + Phát huy năng lực cá nhân.
 + Phát huy năng lực huy động kiến thức.
 Bước 3+4 : Mô tả và xây dựng câu hỏi:
 Mức độ Nhận biết Thông hiểu Vận dụng Vận dụng cao
Nội dung
 Mô tả
 1. Định - Phát biểu (viết ra) - Tìm phần thực, phần - Viết được số 
 nghĩa biểu thức dạng ảo của số phức đã cho. phức khi biết phần 
 số phức. - Mỗi số thực cũng là thực, phần ảo.
 phức - Biết được các một số phức.
 thành phần trong 1 2x 3i 5 (1 3y)i
 Mô tả
3.Biểu Biết biểu diễn số Biết được phần thực là Xác định tập hợp các Dạng phức của chuyển động đều
diễn phức z=a+bi trên hoành độ, phần ảo tung điểm biểu diễn số Z = cost + isint
hình mặt phẳng tọa độ. độ của điểm biểu diễn phức.
học của 
số phức
 Câu hỏi và bài tập
 VD1: Biểu diễn các VD2:Điểm A(3;-2), VD3:
 số phức sau trên O(0;0), B(0;-2) biểu diễn Tìm tập hợp biểu 
 mặt phẳng tọa độ: số phức nào? diễn số phức z
 z = 3 – 2i a) Có phần thực 
 z = 3i bằng-2
 z= -2 b) Phần ảo bằng 
 z = 0 1.
 Mô tả
4. 
Modul Nắm khái niệm Modul là số thực không Tìm được modul của 
số phức modul của số phức âm số phức khi biết số 
 Xác định được modul phức đó.
 của một số phức. Tính độ dài đoạn 
 MN khi biết M,N là 
 hai điểm biểu diễn 
 của hai số phức.
 MN z1 z2
 Câu hỏi và bài tập
 Moodun của số VD1: Số phức 
 phức z a bi Z=1+2i có modul là 1; 5; VD2: Cho VD3: Gọi M,N là điểm biểu diễn 
 3; 5
 z1, z2 .Tìm độ dài MN. Câu hỏi và bài tập
 Ví dụ : Theo quy Hãy tổng quát công thức Ví dụ 1 : Thực hiện Ví dụ2 : Thực hiện phép tính sau:
 tắc cộng, trừ đa thức tính cộng, trừ hai số các phép tính sau: (2i + 3) – (5 – i) + (4 –2i) 
 (coi i là biến), tính: phức? a) (5 + 2i) + (3 – i) Ví dụ 3 : Cho hai số phức z1 = 1 + 
 a) ( 2 + 3i) + (5 + i) b) (2+ 7i) + (– π – 2i)
 2i, z2 = 2 - 3i. Xác định phần thực, 
 b) ( 3 + 5i) – (4 +2 phần ảo của số phức w z z 
 i) 1 2
 (TNTHPT 2010)
 Mô tả
2.Phép Nhận biết phép Giải thích được quy tắc Vận dụng được qui 
nhân số nhân hai số phức. nhân hai số phức. tắc nhân 2 số phức ở + Tính toán được lũy thừa của số 
phức Nêu được “ qui (Thực hiện tương tự mức độ thấp. phức a+bi bậc cao. 
 tắc” nhân hai số nhân hai đa thức(nhị 
 phức (lưu ý i2 1) thức) và thay i2 1)
 Câu hỏi và bài tập
 Ví dụ : Theo quy Tổng quát công thức tính Ví dụ1 : Thực hiện Ví dụ 3: Thực hiện tính:
 tắc nhân đa thức, nhân hai số phức? các phép tính sau: a)(2 3i)2
 2
 a) (3 + 4i)(2 – 3i) 3
 chú ý i = –1, b)(i 1)
 Tính (2 + 3i)(5 – 2i) b) (2i + 3)(7 – i)
 c) 3(5i + 4)
 d) (2 – 4i)5i
 Ví dụ 2: Cho hai số 
 phức z1 = 2 + 5i, = 3 
 –4i. Xác định phần 
 thực, phần ảo của số 
 phức z1.z2
 Mô tả
3.Phép 
chia số Nắm được cách tìm Hiểu được cách thực Thực hiện được Giải phương trình bậc nhất đối với 
phức thương của hai số hiện phép chia hai số phép toán chia hai số z, bài toán tìm phần thực, phần ảo, 
 phức số phức liên hợp, mô đun của số 
 phức. phức phức. Một số bài toán tổng hợp bậc hai 0 không nhất thiết phân 
 với hệ biệt)
 số thực -Biết cách giải pt bậc hai 
 trên tập số phức
 Câu hỏi và bài tập
 VD1. Giải phương VD2. Giải phương trình VD3: . Giải phương VD4. Gọi z1 , z2 là hai nghiệm phức 
 trình sau trên tập số sau trên tập số phức. trình sau trên tập số của phương trình z 2 2z 10 0 .
 phức. a) 7z 2 3z 2 0 phức. Tính giá trị của biểu thức 
 a) z 2 4 0 b) z 4 z 2 1 0 z 3 3z 2 3z 63 0 2 2
 A z1 z2 (ĐH KA -2009)
 b) z 2 z 1 0
 VD5. Tìm số phức z thỏa mãn
 (z i) 4 4z 2 0
Bước 5: Tổ chức các hoạt động học tập
Thời gian : 7 tiết
 Hoạt động Mục đích Nội dung Phương Hình thức
 pháp,kỷ 
 thuật tổ 
 chức
 - Nắm được định nghĩa số VD1: Tìm thực, phần ảo của mỗi Vấn đáp gợi Tại lớp
 phức. số phức sau: mở
 - Biết được các thành phần z 2 3i; z 1 3i
 1 2 
 Hoạt động 1 trong biểu thức số phức: phần z3 2 0.i; z4 0 5i
 thực, phần ảo, số i. VD2: Tìm số thực x,y thỏa:
 - Biết kí hiệu tập số phức b) 3x+1+(3y-2)i = x-yi
 - Biết định nghĩa hai số phức 1 2x 3i 5 (1 3y)i
 bằng nhau. Làm VD 1,2,3 mục 3
 -Biết biểu diễn số phức z=a+bi 
 Tiết 1 trên mặt phẳng tọa độ.
 -Biết khái niệm modul của Làm VD 2 mục 4, VD 1,2,3 mục 5 - Vấn đápgợi Tại lớp
 Hoạt động 2 số phức, tìm mô đun số mở
 phức - Thảo luận 
 -Biết định nghĩa số phức nhóm Hoạt động 1 +Nắm được cách tìm thương Vấn đáp gợi Tại lớp
 của hai số phức. Ví dụ1 : Thực hiện các phép tính mở, hoạt 
 sau: động nhóm
 3 2i 1 i 2 2i
 a) b) c)
 2 3i 2i 5 2 2i
Tiết 4
 Hoạt động 2 Làm 1 số bài tập vận dụng VD2. Tìm nghịch đảo của số phức - Vấn đápgợi Tại lớp 
 kiến thức z biết. mở
 a) z 1 2i b) z 3 i
 VD3.Tìm số phức z thỏa mãn: 
 (3 2i)z (4 5i) 7 3i
 Hoạt động 1 Vận dụng quy tắc cộng trừ, -Làm bài tập 1,3,4 SGKtrang 138 - Vấn đápgợi Tại lớp
 nhân ,chia số phức vào giải mở
 các bài tập Gọi hs lên 
 bảng thực 
 hiện
 Luyện tập các bài toán nâng BT1: Cho số phức z thỏa mãn - Vấn đápgợi Tại lớp
 cao (1 + i)z – 2 – 4i = 0 . Tìm số phức mở
Tiết 5 Hoạt động 2 liên hợp của z. (TNTHPT 2013) . - Thảo luận 
 BT2: Tìm mô đun của số phức z nhóm
 biết
 (2 + i)z + 3 z = 11 – i 
 1 3
 Ví dụ: Cho z i . Hãy 
 2 2
 1 3
 tính , z2 , z , 1 z z2
 z